Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔDAH có DI/DH=DO/DA
nen Io//AH và IO=AH/2
=>AH=2OI
a, Xét tứ giác HFEB có:
\(\widehat{FHB}+\widehat{FEB}=90+90=180^0\)
--> Tứ giác HFEB nội tiếp
b, Dùng hệ thức lượng trong \(\Delta ABC\) vuông
\(AC^2=AH.AB\)
Mà \(\Delta AHF=\Delta AEB\left(tự.chứng.minh\right)\left(g-g\right)\)
\(\Rightarrow\dfrac{AH}{AE}=\dfrac{AF}{AB}\Rightarrow AH.AB=AE.AF\\ \Rightarrow AC^2=AE.AF\)
c, Ta có AICK là tứ giác nội tiếp \(\left(\widehat{ACK}+\widehat{IKA}=180^0\right)\)
\(\widehat{IKb}+\widehat{IEB}=180^0\\ \Rightarrow\widehat{AIK}+\widehat{EIK}=\widehat{EIK}+\widehat{EBA}=180^0\\ \Rightarrow\widehat{AIK}=\widehat{EBA}\\ \Rightarrow\widehat{ACK}=\widehat{EBA}\\ Tương.tự.ta.có:\widehat{CAO}=\widehat{KEB}\\ \Rightarrow\Delta ACK=\Delta EBK\left(g-g\right)\)
\(\rightarrow\dfrac{AC}{EB}=\dfrac{CK}{KB}=\dfrac{AK}{EK}\Rightarrow EK.CK=AK.KB\\ =\dfrac{\left(EK+KC\right)^2}{4}=\dfrac{\left(AK+KB\right)^2}{4}=\dfrac{AB^2}{4}\\ \Rightarrow EK+KC=AB\\ Dấu"="\Leftrightarrow\\ EA=KC\Rightarrow\Delta CKE.cân.tại.K\\ \Rightarrow Sđ\widehat{BE}=Sđ\widehat{AC}\\ \Rightarrow E\in\widehat{BC}.sao.cho.Sđ\widehat{BE}=Sđ\widehat{AC}.hay.BE=AC\)
1. Xét tam giác AEB có: AB là đường kính \(\Rightarrow\Delta AEB\) vuông tại E
Xét tứ giác HFEB có: \(\left\{{}\begin{matrix}\widehat{FHB}=90^o\\\widehat{FEB}=90^o\end{matrix}\right.\)\(\Rightarrow\widehat{FHB}+\widehat{FEB}=180^o\)
\(\Rightarrow\)Tứ giác HFEB nội tiếp đường tròn (đpcm)
2. Xét tam giác ABC có: đường kính AB \(\Rightarrow\Delta ABC\) vuông tại C
\(\Rightarrow AC^2=AH.AB\)
Mà \(\Delta AHF\sim\Delta AEB\) \(\Rightarrow AC^2=AF.AE\) (đpcm)
3. Câu này mình chịu @@
+ Vì O là giao điểm của ba đường phân giác trong tam giác ABC nên O là tâm của đường tròn nội tiếp tam giác ABC nên đáp án A sai.
+ Tam giác ABC vuông tại A có F là trung điểm của BC nên AF là đường trung tuyến ứng với cạnh huyền
Do đó: AF = 1 2 BC (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Suy ra AF = FC = FB
Nên F cách đều ba đỉnh A, B, C
Do đó F là tâm đường tròn ngoại tiếp tam giác ABC.
+ Vì D ≠ E ≠ F và chỉ có một đường tròn ngoại tiếp tam giác ABC nên đáp án B, C sai và D đúng.
Chọn đáp án D
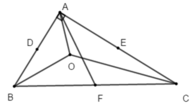
a: Xét ΔABC vuông tại B có BK là đường cao
nên \(\dfrac{1}{BK^2}=\dfrac{1}{BA^2}+\dfrac{1}{BC^2}\)
hay BK=4,8cm
b: Xét ΔABC vuông tại B có BK là đường cao
nên \(AK\cdot AC=BA^2\)
\(\Leftrightarrow AK\cdot AC=\left(2\cdot AI\right)^2=4\cdot AI^2\)