Cho tam giác DEF vuông tại D \(\dfrac{DE}{DF}\)= 0,3, EF= 15cm. Tính DF?
Xin cảm ơn mn ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
1
22 tháng 3 2022
Áp dụng định lí Pytago ta có
\(DE^2=DF^2+FE^2\\ \Rightarrow DF=\sqrt{15^2-12^2}=9\)
TM
1
YP
22 tháng 3 2022
Xét tam giác DEF vuông tại F có:
\(DE^2=EF^2+DF^2\) (Định lý Pytago)
=> \(15^2=12^2+DF^2\)
=> 225 = 144 + \(DF^2\)
=> \(DF^2=\) 225-144 = 81
=> DF = \(\sqrt{81}\) = 9
LD
2 tháng 4 2022
Xét ΔDEF vuông ở D , theo định lý Pi-ta-go ta được :
\(\Rightarrow EF=\sqrt{DE^2+DF^2}=\sqrt{15^2+20^2}=25\left(cm\right)\)
Ta có : DI là phân giác \(\widehat{EDF}\)
\(\Rightarrow\dfrac{EI}{IF}=\dfrac{DE}{DF}\)
hay \(\dfrac{EI}{IF}=\dfrac{15}{20}=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{EI}{3}=\dfrac{IF}{4}=\dfrac{EI+IF}{3+4}=\dfrac{25}{7}\)
\(\Rightarrow EI=\dfrac{25}{7}.3=\dfrac{75}{7}\left(cm\right)\)
\(\Rightarrow FI=\dfrac{25}{7}.4=\dfrac{100}{7}\left(cm\right)\)
25 tháng 1
Sửa đề; DH vuông góc EF tại H
a: Xét ΔDHE vuông tại H và ΔDHF vuông tại H có
DE=DF
DH chung
Do đó: ΔDHE=ΔDHF
=>HE=HF
b: Ta có: HE=HF
H nằm giữa E và F
Do đó: H là trung điểm của EF
=>\(HE=HF=\dfrac{EF}{2}=4\left(cm\right)\)
ΔDHE vuông tại H
=>\(DH^2+HE^2=DE^2\)
=>\(DH^2=5^2-4^2=9\)
=>\(DH=\sqrt{9}=3\left(cm\right)\)
c: Ta có: \(DM=MF=\dfrac{DF}{2}\)
\(DN=NE=\dfrac{DE}{2}\)
mà DF=DE
nên DM=MF=DN=NE
Xét ΔDME và ΔDNF có
DM=DN
\(\widehat{MDE}\) chung
DE=DF
Do đó: ΔDME=ΔDNF
=>EM=FN và \(\widehat{DEM}=\widehat{DFN}\)
d: Xét ΔNEF và ΔMFE có
NE=MF
NF=ME
EF chung
Do đó: ΔNEF=ΔMFE
=>\(\widehat{NFE}=\widehat{MEF}\)
=>\(\widehat{KEF}=\widehat{KFE}\)
=>ΔKEF cân tại K
3 tháng 10 2021
\(a,\) Áp dụng Pytago \(EF=\sqrt{DE^2+DF^2}=25\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}DE^2=EH\cdot EF\\DF^2=FH\cdot EF\\DH^2=FH\cdot EH\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}EH=\dfrac{DE^2}{EF}=9\left(cm\right)\\FH=\dfrac{DF^2}{EF}=16\left(cm\right)\\DH=\sqrt{9\cdot16}=12\left(cm\right)\end{matrix}\right.\)
\(b,\sin\widehat{E}=\cos\widehat{F}=\dfrac{DF}{EF}=\dfrac{4}{5}\approx\left\{{}\begin{matrix}\sin53^0\\\cos37^0\end{matrix}\right.\\ \Rightarrow\widehat{E}\approx53^0;\widehat{F}\approx37^0\)
26 tháng 3 2023
\(\text{#TNam}\)
`a,` Xét Tam giác `HED` và Tam giác `HFD` có
`DE = DF (\text {Tam giác DEF cân tại D})`
\(\widehat{E}=\widehat{F}\) `(\text {Tam giác DEF cân tại D})`
`=> \text {Tam giác HED = Tam giác HDF (ch-gn)}`
`b,` Vì Tam giác `HED =` Tam giác `HFD (a)`
`-> HE = HF (\text {2 cạnh tương ứng})`
Xét Tam giác `HEM` và Tam giác `HFN` có:
`HE = HF (CMT)`
\(\widehat{E}=\widehat{F}\) `(a)`
\(\widehat{EMH}=\widehat{FNH}=90^0\)
`=> \text {Tam giác HEM = Tam giác HFN (ch-gn)}`
`-> EM = FN (\text {2 cạnh tương ứng})`
Ta có: \(\left\{{}\begin{matrix}DE=MD+ME\\DF=ND+NF\end{matrix}\right.\)
Mà `DE = DF, ME = NF`
`-> MD = ND`
Xét Tam giác `DMN: DM = DN (CMT)`
`-> \text {Tam giác DMN cân tại D}`
`->`\(\widehat{DMN}=\widehat{DNM}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `DEF` cân tại `D`
`->`\(\widehat{E}=\widehat{F}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{DMN}=\widehat{E}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {MN // EF (t/c 2 đt' //)}`
KH
11 tháng 2 2017
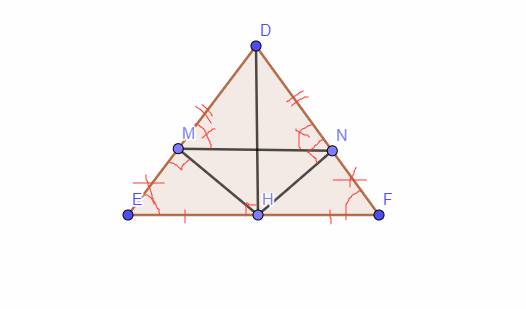
Giải:
Áp dụng định lý Py-ta-go vào tam giác HDF, ta có:
HF2 + DH2 = DF2
=> 162 + DH2 = 202
=> DH2 = 144 = 122
=> DH = 12 (cm)
Áp dụng định lý Py-ta-go vào tam giác DEH có:
DE2 = 92 + 122 = 225 = 152
=> DE = 15 (cm)
TL
11 tháng 2 2017
áp dụng định lý pitago vào tam giác DHF ta có:
HF2 + DH2 = DF2
hay 162+ DH2 = 202
suy ra : DH2= 144 =122
suy ra: DH = 12
áp dụng định lý pitago vào tam giác DEH ta có :
DE2 = 92+122= 225 = 152
suy ra : DE = 15
Ta có: \(tanDFE=\dfrac{DE}{DF}=0,3\Rightarrow\widehat{DFE}\approx16^o42'\)
\(\Rightarrow DF=sinDFE.EF=sin16^o42'.15=4,31\left(cm\right)\)