Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
MN // QP (cùng song song với BC)
MN = QP ( =1/2 BC)
⇒ MNPQ là hình bình hành.
Hình thang ABCD là hình thang cân có hai góc kề một đáy đều bằng 45 0 thì MNPQ là hình vuông.
MNPQ là hình thoi vì là hình bình hành có hai cạnh kề bằng nhau.
a: Xét ΔABC có
M là trung điểm của AB
P là trung điểm của AC
Do đó: MP là đường trung bình của ΔABC
Suy ra: MP//BC và \(MP=\dfrac{BC}{2}\left(1\right)\)
Xét ΔBDC có
Q là trung điểm của BD
N là trung điểm của DC
Do đó: QN là đường trung bình của ΔBDC
Suy ra: QN//BC và \(QN=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra QN//MP và QN=MP
hay MQNP là hình bình hành
a / hình bình hành
b/ AC=BD ; AB>CD ; AB<AC<CD;AB<BD<CD
c/hình vuông
(Hình thì bạn tự vẽ nha)
a) Xét tam giác BAD có: MB=MA ; QB=QD
=> MQ là đường trung bình của tam giác BAD
=> MQ // AD ; MQ = 1/2 AD (1)
Xét tam giác CAD có: NC = NA ; PC = PD
=> NP là đường trung bình của tam giác CAD
=> NP // AD ; NP = 1/2 AD (2)
Từ (1), (2) => MQ // NP ; MQ = NP
Tứ giác MNPQ có: MQ // NP ; MQ = NP
=> MNPQ là hình bình hành
b) Theo a), ta có: MQ = 1/2 AD (*)
Xét tam giác ABC có: MA = MB ; NA = NC
=>MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC (**)
Từ (*), (**) và AD=BC (ABCD là thang cân)
=> MQ = MN
Hình bình hành MNPQ có MQ = MN
=> MNPQ là hình thoi
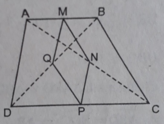
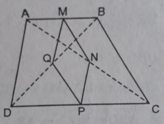
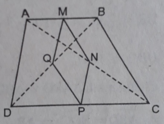
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2(1)
Xét ΔBDC có
Q là tđiểm của BD
P là tđiểm của CD
Do đó: QP là đường trung bình
=>QP//BC và QP=BC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hbh
b: Xét ΔABD có
M là tđiểm của AB
Q là tđiểm của BD
Do đó: MQ là đường trung bình
=>MQ=AD/2=BC/2(3)
Từ (2) và (3) suy ra MQ=QP
hay MNPQ là hình thoi