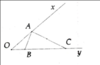
cho góc xOy, trên tia Ox lấy điểm Á sao cho OA = 4cm, trên tia Oy lấy hai điểm B và C sao cho OB = 2cm, OC = 8cm. Chứng minh rằng tam giác AOB ~ tam giác COA.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

12 tháng 3 2023
a: Xet ΔOCB và ΔOAD có
OC/OA=OB/OD
góc O chung
=>ΔOCB đồng dạng với ΔOAD
b: ΔOCB đồng dạng với ΔOAD
=>góc OCB=góc OAD
=>góc IAB=góc ICD
=>góc IBA=góc IDC; góc AIB=góc CID

12 tháng 3 2023
a: Xet ΔOCB và ΔOAD có
OC/OA=OB/OD
góc O chung
=>ΔOCB đồng dạng với ΔOAD
b: ΔOCB đồng dạng với ΔOAD
=>góc OCB=góc OAD
=>góc IAB=góc ICD
=>góc IBA=góc IDC; góc AIB=góc CID

HN
2 tháng 12 2021
a: Xét ΔOAD và ΔOCB có
OA=OC
ˆOO^ chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB
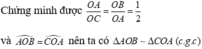
Bổ sung ĐK : ^xOy \(\ne\)1800
Xét tam giác AOB và tam giác COA ta có :
O _ chung
\(\frac{OA}{OC}=\frac{OB}{OA}=\frac{4}{8}=\frac{2}{4}=\frac{1}{2}\)
Vậy tam giác AOB ~ tam giác COA ( c.g.c )