cho tam giác ABC.Qua trung điểm D của BC kẻ đường thẳng song song với AB. Nó cắt AC tại E. Qua E kẻ Đường thẳng song song với BC. Nó cắt AB tại F. Chứng minh rằng:tam giác CDE = tam giác EFA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2022
a: Xét tứ giác BFED có
ED//BF
FE//BD
Do đó: BFED là hình bình hành
Xét ΔABC có
D là trung điểm của BC
DE//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
EF//CB
Do đó: F là trung điểm của AB
Xét ΔCDE và ΔEFA có
CD=EF
DE=FA
CE=EA
Do đó: ΔCDE=ΔEFA
b: Gọi ΔABC có F là trung điểm của AB,E là trung điểm của AC
Trên tia FE lấy điểm E sao cho E là trung điểm của FK
Xét tứ giác AFCK có
E là trung điểm của AC
E là trung điểm của FK
Do đó: AFCK là hình bình hành
Suy ra: AF//KC và KC=AF
hay KC//FB và KC=FB
Xét tứ giác BFKC có
KC//FB
KC=FB
Do đó: BFKC là hình bình hành
Suy ra: FE//BC(ĐPCM)
CM
10 tháng 12 2018
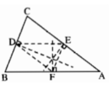
+)Xét tam giác BDF và ∆EFD có:
DF chung
∠BDF = ∠DFE ( hai góc so le trong; BC// EF)
∠BFD = ∠FDE ( hai góc so le trong; DE// AB)
Suy ra:∆ BDF = ∆EFD (g.c.g)
Suy ra BD = EF. Theo giả thiết, D là trung điểm của BC nên CD = DB = EF.
+) Xét ∆ CDE và ∆ EFA có :
CD = EF ( chứng minh trên)
∠(CDE) = ∠(EFA) = ∠(CBA)
∠(ECD) = ∠(AEF) (các góc đồng vị).
Suy ra: ∆ CDE = ∆ EFA ( g.c.g)
Suy ra CE = EA nên E là trung điểm của CD.
19 tháng 12 2020
Cứng đờ tay luôn rồi, khổ quá:((
a) Xét \(\Delta DBF\) và \(\Delta FED:\)
DF:cạnh chung
\(\widehat{BDF}=\widehat{EFD}\)(AB//EF)
\(\widehat{BFD}=\widehat{EDF}\)(DE//BC)
=> \(\Delta BDF=\Delta EFD\left(g-c-g\right)\)
b) (Ở lớp 8 thì sé có cái đường trung bình ý bạn, nó sẽ có tính chất luôn, nhưng lớp 7 chưa học đành làm theo lớp 7 vậy)
Ta có: \(\widehat{DAE}+\widehat{AED}+\widehat{EDA}=180^o\) (Tổng 3 góc trong 1 tam giác)
Lại có: \(\widehat{AED}+\widehat{DEF}+\widehat{FEC}=180^o\)
Mà \(\widehat{DEF}=\widehat{EDA}\)(AB//EF)
=>\(\widehat{DAE}=\widehat{FEC}\)
Xét \(\Delta DAE\) và \(\Delta FEC:\)
DA=FE(=BD)
\(\widehat{DAE}=\widehat{EFC}\left(=\widehat{DBF}\right)\)
\(\widehat{DAE}=\widehat{FEC}\) (cmt)
=>\(\Delta DAE=\Delta FEC\left(g-c-g\right)\)
=> DE=FC(2 cạnh t/ứ)
=> Đpcm
17 tháng 10 2019
NGU NHƯ BÒÔFÔFÒÔFÔFÔFFÒÔFFÔFOFOFÔFỒ
RỨA MÀ KHÔNG LÀM ĐƯỢC NGU VL NGU VCL NGU VÃI LINH HỒN NGU VÃI L*N CHIM ÉN
xet tam giac BDF va tam giac DEF ta co
DF=DF ( canh chung)
goc BDF = goc DFE ( 2 goc sole trong va BA//EF)xet tam giac BDF va tam giac DEF ta co
DF=DF ( canh chung)
goc BDF = goc DFE ( 2 goc sole trong va BA//EF)
goc DFB = goc FDE ( 2 goc sole trong va DE//BC)
--> tam giac BDF = tam giac DEF ( g-c-g)
--> BD= EF ( 2 goc tuong ung)
ma AD=BD ( D la trung diem AB)
nen AD=EF
b)ta co
goc ADE=goc BAC ( 2 goc dong vi va DE//BC)
goc CEF = goc BAC ( 2 goc dong vu va EF//AB)
--> goc ADE = goc CFE
xet tam giac ADE va tam giac EFC ta co
goc ADE=goc CFE ( cmt
AD= EF ( cm a)
goc DAE = goc FEC ( 2 goc dong vi va DE//BC)
--> tam giac ADE = tam giac EFC ( c-g-c)
c) tam giac ADE= tam giac EFC (cmt)--> AE=EC
goc DFB = goc FDE ( 2 goc sole trong va DE//BC)
--> tam giac BDF = tam giac DEF ( g-c-g)
--> BD= EF ( 2 goc tuong ung)
ma AD=BD ( D la trung diem AB)
nen AD=EF
b)ta co
goc ADE=goc BAC ( 2 goc dong vi va DE//BC)
goc CEF = goc BAC ( 2 goc dong vu va EF//AB)
--> goc ADE = goc CFE
xet tam giac ADE va tam giac EFC ta co
goc ADE=goc CFE ( cmt
AD= EF ( cm a)
goc DAE = goc FEC ( 2 goc dong vi va DE//BC)
--> tam giac ADE = tam giac EFC ( c-g-c)
c) tam giac ADE= tam giac EFC (cmt)--> AE=EC
4 tháng 1 2022
a: Xét tứ giác BDEF có
DE//BF
BD//EF
Do đó: BDEF là hình bình hành
Suy ra: EF=BD
mà BD=AD
nên EF=AD
b: Xét ΔADF và ΔFEA có
AD=FE
AF chung
DF=EA
Do đó: ΔADF=ΔFEA
12 tháng 12 2021
Gọi Bx là tia đối của tia BA. Lấy E trên AC sao cho AB = AE
Xét tam giác BAD=EAD c-g-c => BD = DE và DEC = CBx
Trong tam giác ABC, BAC + ABC + ACB = 180 => ACB = 180 - BAC - ABC => ACB < 180 - ABC
Ta có DBx + ABC = 180 (hai góc kề bù) => DBx = 180 - ABC
=>ACB < DBx => ACB < DEC => Trong tam giác DEC, DC > DE (Quan hệ giữa góc và cạnh)
Vậy BD < DC
ta có: EF//BD
FB//ED
suy ra; EB=ED; EF=BD
mà DB=DC suy ra EF=DC
6F1=^B( 2 góc đồng vị)
^B=^D1( 2 góc đồng vị)
suy ra ^F1=^D1
ta có: ^E1=^D2(2 góc đồng vị)
^C=^D2( 2 góc đồng vị)
suy ra ^E1=^C
xét tam giác CDE và tam giác EFA có:
EF=DC(cmt)
^F1=^D1(cmt)
^E1=^C(cmt)
suy ra tam giác CDE=tam giác EFA(g.c.g)
ta có: EF//BD
FB//ED
suy ra; EB=ED; EF=BD
mà DB=DC suy ra EF=DC
6F1=^B( 2 góc đồng vị)
^B=^D1( 2 góc đồng vị)
suy ra ^F1=^D1
ta có: ^E1=^D2(2 góc đồng vị)
^C=^D2( 2 góc đồng vị)
suy ra ^E1=^C
xét tam giác CDE và tam giác EFA có:
EF=DC(cmt)
^F1=^D1(cmt)
^E1=^C(cmt)
suy ra tam giác CDE=tam giác EFA(g.c.g)