cho tam giác abc nhọn nội tiếp (o r) Các đường cao ad,ce cắt nhau tại h chứng minh tứ giác behd,aedc nội tiếp,ae.eb=eh.ec
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 9 2018
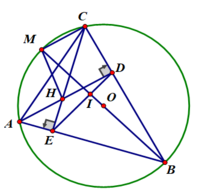
a) Xét tứ giác AEDC có:
∠(AEC) = ∠(ADC) = 90 0
Mà 2 góc này cùng nhìn cạnh AC
⇒ Tứ giác AEDC là tứ giác nội tiếp
1 tháng 4 2021
a) Xét tứ giác AEDC có
\(\widehat{AEC}=\widehat{ADC}\left(=90^0\right)\)
\(\widehat{AEC}\) và \(\widehat{ADC}\) là hai góc cùng nhìn cạnh AC
Do đó: AEDC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
21 tháng 8 2022
a: Xéttứ giác AEHF có góc AEH+góc AFH=180 độ
nên AEHF là tứ giác nội tiếp
c: Xét tứ giác AEDC có góc ADC=góc AEC=90 độ
nên AEDC là tứ giác nội tiếp
d: góc EDA=góc ABF
góc FDA=góc FDH=góc ACE
mà góc ABF=góc ACE
nên góc EDA=góc FDA
=>DA là phân giác của góc EDF
6 tháng 5 2020
em lớp 6 nên ko trả lời đc xin lỗi chị nha chúc chị học tốt
a) Xét tứ giác BEHD có
\(\widehat{BEH}\) và \(\widehat{BDH}\) là hai góc đối
\(\widehat{BEH}+\widehat{BDH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BEHD là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)