ko cần làm câu a đâu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu b bạn tự vẽ
Câu c:
PT hoành độ giao điểm: \(-3x+1=\left(1-2m\right)x+m-1\)
Mà 2 đt cắt tại hoành độ 1 nên \(x=1\)
\(\Leftrightarrow-2=1-2m+m-1\Leftrightarrow m=2\)
Câu d:
PT giao Ox,Oy lần lượt tại A,B của (d) là:
\(\left\{{}\begin{matrix}y=0\Rightarrow x=\dfrac{m-1}{2m-1}\Rightarrow A\left(\dfrac{m-1}{2m-1};0\right)\Rightarrow OA=\left|\dfrac{m-1}{2m-1}\right|\\x=0\Rightarrow y=m-1\Rightarrow B\left(0;m-1\right)\Rightarrow OB=\left|m-1\right|\end{matrix}\right.\)
Gọi H là chân đường cao từ O đến (d)
Đặt \(OH^2=t\)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{\left(2m-1\right)^2}{\left(m-1\right)^2}+\dfrac{1}{\left(m-1\right)^2}\)
\(\Leftrightarrow\dfrac{1}{t}=\dfrac{4m^2-4m+2}{\left(m-1\right)^2}\Leftrightarrow t=\dfrac{m^2-2m+1}{4m^2-4m+2}\\ \Leftrightarrow4m^2t-4mt+2t=m^2-2m+1\\ \Leftrightarrow m^2\left(4t-1\right)+2m\left(1-2t\right)+2t-1=0\)
Coi đây là PT bậc 2 ẩn m, PT có nghiệm
\(\Leftrightarrow\Delta'=\left(1-2t\right)^2-\left(4t-1\right)\left(2t-1\right)\ge0\\ \Leftrightarrow4t^2-4t+1-8t^2+6t-1\ge0\\ \Leftrightarrow2t-4t^2\ge0\\ \Leftrightarrow2t\left(1-2t\right)\ge0\\ \Leftrightarrow0\le t\le\dfrac{1}{2}\)
\(\Leftrightarrow OH^2\le\dfrac{1}{2}\Leftrightarrow OH\le\dfrac{1}{\sqrt{2}}\)
Dấu \("="\Leftrightarrow\dfrac{m^2-2m+1}{4m^2-4m+2}=\dfrac{1}{2}\Leftrightarrow4m^2-4m+2=2m^2-4m+2\)
\(\Leftrightarrow2m^2=0\Leftrightarrow m=0\)
Vậy m=0 thỏa yêu cầu đề

1: \(\Leftrightarrow x-2-7x+7=-1\)
=>-6x+5=-1
hay x=1(loại)
3: \(\Leftrightarrow\left(x+2\right)\left(x-1\right)-\left(x+1\right)\left(x+3\right)=4\)
\(\Leftrightarrow x^2+x-2-x^2-4x-3=4\)
=>-3x=9
hay x=-3(loại)
4: \(\Leftrightarrow x^2+2x+1-x^2+2x-1=3x\cdot\dfrac{x+1-x+1}{x+1}\)
\(\Leftrightarrow4x=\dfrac{6x}{x+1}\)
\(\Leftrightarrow4x^2+4x-6x=0\)
\(\Leftrightarrow4x^2-2x=0\)
=>2x(2x-1)=0
hay \(x\in\left\{0;\dfrac{1}{2}\right\}\)

Câu 1:
a, Dẫn từng khí qua dd Ca(OH)2.
+ Xuất hiện kết tủa trắng: CO2
PT: \(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_{3\downarrow}+H_2O\)
+ Không hiện tượng: C2H4 và CH4. (1)
- Dẫn khí nhóm (1) qua dd Brom dư.
+ Dd Brom nhạt màu dần: C2H4.
PT: \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
+ Không hiện tượng: CH4.
b, - Dẫn từng khí qua dd Ca(OH)2 dư.
+ Xuất hiện kết tủa trắng: SO2
PT: \(SO_2+Ca\left(OH\right)_2\rightarrow CaSO_{3\downarrow}+H_2O\)
+ Không hiện tượng: C2H2 và CO. (1)
- Dẫn khí nhóm (1) qua dd Brom dư.
+ Dd Brom nhạt màu dần: C2H2.
PT: \(C_2H_2+2Br_2\rightarrow C_2H_2Br_4\)
+ Không hiện tượng: CO.
c, - Dẫn từng khí qua quỳ tím ẩm.
+ Quỳ tím hóa đỏ rồi mất màu: Cl2
PT: \(Cl_2+H_2O⇌HCl+HClO\)
+ Quỳ tím hóa đỏ: HCl
+ Quỳ tím hóa hồng: CO2
PT: \(CO_2+H_2O⇌H_2CO_3\)
+ Quỳ tím không đổi màu: CO2
Câu 2:
a, Dẫn hh khí qua dd Brom dư, C2H4 và C2H2 được giữ lại, ta thu được CH4.
PT: \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
\(C_2H_2+2Br_2\rightarrow C_2H_2Br_4\)
b, - Dẫn hh khí qua dd Ca(OH)2 dư, CO2 bị giữ lại.
PT: \(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)
- Tiếp tục dẫn hh khí qua dd Brom dư, C2H4 bị giữ lại, khí thoát ra sau pư là CH4.
PT: \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)

Câu 1:
PT: \(Na_2CO_3+H_2SO_4\rightarrow Na_2SO_4+CO_2+H_2O\)
\(2NaHCO_3+H_2SO_4\rightarrow Na_2SO_4+2CO_2+2H_2O\)
Gọi: \(\left\{{}\begin{matrix}n_{Na_2CO_3}=x\left(mol\right)\\n_{NaHCO_3}=y\left(mol\right)\end{matrix}\right.\) ⇒ 106x + 84y = 9,1 (1)
Theo PT: \(n_{CO_2}=n_{Na_2CO_3}+n_{NaHCO_3}=x+y=\dfrac{2,016}{22,4}=0,09\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}x=0,07\left(mol\right)\\y=0,02\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m_{Na_2CO_3}=0,07.106=7,42\left(g\right)\\m_{NaHCO_3}=0,02.84=1,68\left(g\right)\end{matrix}\right.\)
Theo PT: \(n_{H_2SO_4}=n_{Na_2CO_3}+\dfrac{1}{2}n_{NaHCO_3}=0,08\left(mol\right)\)
\(\Rightarrow m_{H_2SO_4}=0,08.98=7,84\left(g\right)\Rightarrow m_{ddH_2SO_4}=\dfrac{7,84}{50\%}=15,68\left(g\right)\)
Câu 2:
Ta có: m bình 1 tăng = mH2O = 3,6 (g)
\(\Rightarrow n_{H_2O}=\dfrac{3,6}{18}=0,2\left(mol\right)\)
m bình 2 tăng = mCO2 = 13,2 (g)
\(\Rightarrow n_{CO_2}=\dfrac{13,2}{44}=0,3\left(mol\right)\)
PT: \(C_2H_4+3O_2\underrightarrow{t^o}2CO_2+2H_2O\)
\(2C_2H_2+5O_2\underrightarrow{t^o}4CO_2+2H_2O\)
Theo PT: \(\left\{{}\begin{matrix}n_{CO_2}=2n_{C_2H_4}+2n_{C_2H_2}=0,3\left(mol\right)\\n_{H_2O}=2n_{C_2H_4}+n_{C_2H_2}=0,2\left(mol\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n_{C_2H_4}=0,05\left(mol\right)\\n_{C_2H_2}=0,1\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{C_2H_4}=\dfrac{0,05.28}{0,05.28+0,1.26}.100\%=35\%\\\%m_{C_2H_2}=65\%\end{matrix}\right.\)

Câu 3:
Ta có: \(n_{C_2H_4}+n_{C_2H_2}=\dfrac{5,6}{22,4}=0,25\left(mol\right)\left(1\right)\)
PT: \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
\(C_2H_2+2Br_2\rightarrow C_2H_2Br_4\)
Theo PT: \(n_{Br_2}=n_{C_2H_4}+2n_{C_2H_2}=\dfrac{56}{160}=0,35\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{C_2H_4}=0,15\left(mol\right)\\n_{C_2H_2}=0,1\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%V_{C_2H_4}=\dfrac{0,15.22,4}{5,6}.100\%=60\%\\\%V_{C_2H_2}=40\%\end{matrix}\right.\)


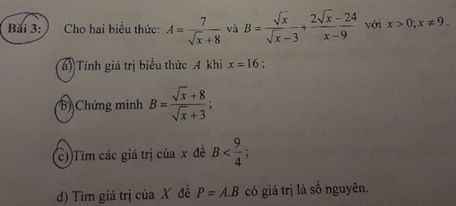




 Làm hộ mình câu 5 thôi nhé !
Làm hộ mình câu 5 thôi nhé !
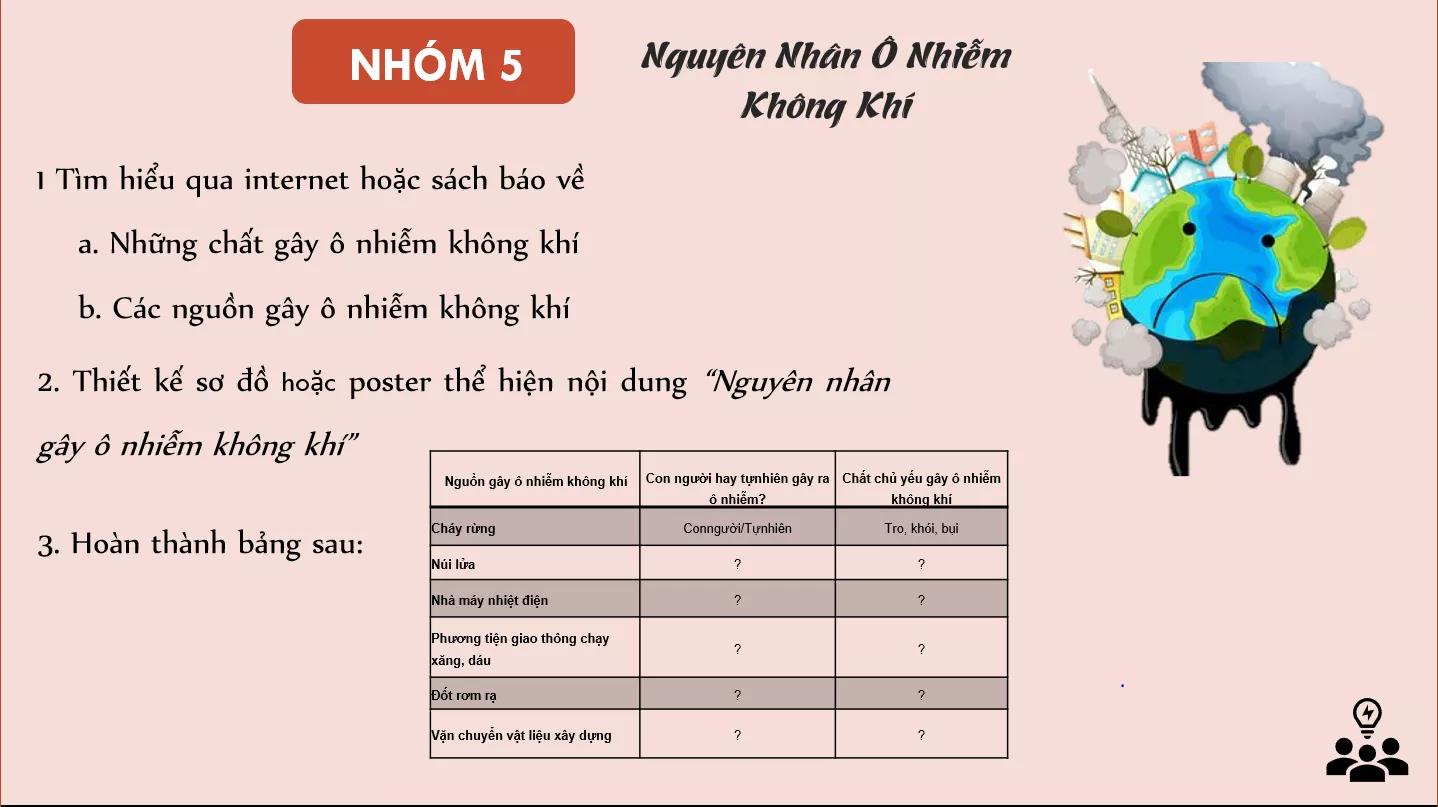 làm giúp mk các câu hỏi này nha ko cần poster đâu
làm giúp mk các câu hỏi này nha ko cần poster đâu hình ko cần vẽ đâu ạ, em vẽ rồi. Làm giúp em câu 2b thôi
hình ko cần vẽ đâu ạ, em vẽ rồi. Làm giúp em câu 2b thôi
a: \(=\dfrac{1}{5}-\dfrac{9}{5}+1=1-\dfrac{8}{5}=-\dfrac{3}{5}\)
Cho tam giác HIK có HI = HK. Gọi M là Trung điểm của IK
a) vẽ hình, viết giả thiết, kết luận của bài toán
b) chứng minh : tam giác HIM = Tam giác HKM.
c) chứng minh : HM là tia phân giác HIK