Giải hộ mình với
Cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(=\dfrac{x^2+x-2x+2-2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-x}{\left(x-1\right)\left(x+1\right)}=\dfrac{x}{x+1}\)

a) \(x^2+2x+3=\left(x^2+2x+1\right)+2=\left(x+1\right)^2+2\ge2\)
Dấu "=" xảy ra khi \(\left(x+1\right)^2+2=2\Rightarrow x=-1\)
Vậy \(MinA=2\)khi \(x=-1\)
c) \(4x^2-4x+5=\left(4x^2-4x+1\right)+4=\left(2x-1\right)^2+4\ge4\)
Dấu "=" xảy ra khi \(\left(2x-1\right)^2+4=4\Rightarrow x=\dfrac{1}{2}\)
Vậy \(MinC=4\) khi \(x=\dfrac{1}{2}\)

a: để \(\dfrac{4}{x}>\dfrac{4}{5}\\ \Rightarrow x< 5\)
mà x là các số tự nhiên
\(\Rightarrow x\in\left\{1;2;3;4\right\}\)
b: để \(\dfrac{1}{9}< \dfrac{x}{9}< \dfrac{4}{9}th\text{ì}1< x< 4\\ \Rightarrow x\in\left\{2;3\right\}\)
A) x>5 => x=1,x=2,x=3,x=4 do hai tử bằng nhau thì phân số nào có mẫu nhỏ hơn sẽ lớn hơn
B) x=2 hoặc x= 3
C) x=7

\(a,\Rightarrow x-2=8\\ \Rightarrow x=10\\ b,\Rightarrow x+12-17=20\\ \Rightarrow x-5=20\\ \Rightarrow x=25\\ c,\Rightarrow11-\left(4x+5\right):3=4\\ \Rightarrow\left(4x+5\right):3=7\\ \Rightarrow4x+5=21\\ \Rightarrow x=4\\ d,\Rightarrow\left(35:x+3\right)\cdot17=136\\ \Rightarrow35:x+3=8\\ \Rightarrow35:x=5\\ \Rightarrow x=7\\ e,\Rightarrow41-\left(2x-5\right)=720:8\cdot5=180\\ \Rightarrow2x-5=-139\\ \Rightarrow2x=-134\\ \Rightarrow x=-67\)
\(2,\\ a,\Rightarrow x^2=4^3:16=64:16=4=2^2=\left(-2\right)^2\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\\ b,\Rightarrow\left(x-1\right)^2=9=3^2=\left(-3\right)^2\\ \Rightarrow\left[{}\begin{matrix}x-1=3\\x-1=-3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\\ c,\Rightarrow\left(3x-7\right)^5=2^5\\ \Rightarrow3x-7=2\\ \Rightarrow3x=9\Rightarrow x=3\)


a: góc ASB=1/2*180=90 độ=góc ABM
b: ON vuông góc AS
BS vuông góc SA
=>ON//BS
c: góc OIM+góc OBM=180 độ
=>OIMB nội tiếp

1 because
2 as long as
3 although
4 so that
5 although
6 even if
7 until
8 while
9 because
10 Although


\(M=\left(\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right).\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{2\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{2\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
2. Ta có:
\(\sqrt{x}>0\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}+2}>0\) hay \(M>0\)
Lại có: \(M=\dfrac{\sqrt{x}+2-1}{\sqrt{x}+2}=1-\dfrac{1}{\sqrt{x}+2}< 1\)
\(\Rightarrow0< M< 1\Rightarrow M>M^2\)
1) Ta có: \(M=\left(\dfrac{\sqrt{x}}{x-4}+\dfrac{1}{\sqrt{x}-2}\right)\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{\sqrt{x}+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{2\sqrt{x}+2}{2\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
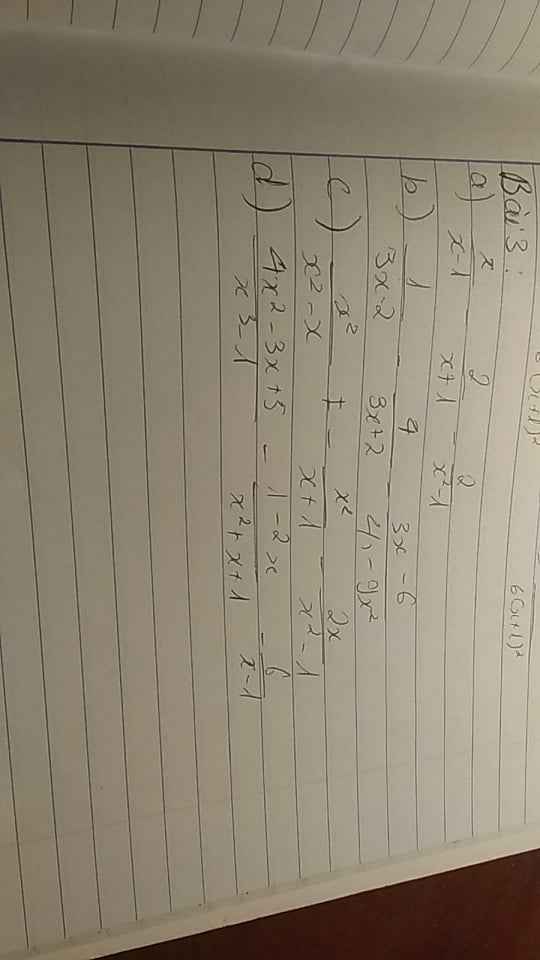



 giải hộ mình với ạ, mình đang cần gấp!
giải hộ mình với ạ, mình đang cần gấp!


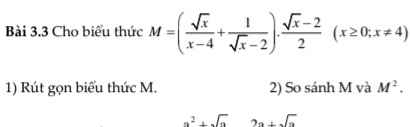
Điện trở tương đương của đoạn mạch là:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{20.30}{20+30}=12\left(\Omega\right)\)
Do mắc song song nên \(U=U_1=U_2=24V\)
Cường độ dòng điện chạy qua mạch chính là:
\(I=\dfrac{U}{R_{tđ}}=\dfrac{24}{12}=2\left(A\right)\)
Do mắc nối tiếp nên \(I_3=I_2=\dfrac{U_2}{R_2}=\dfrac{24}{30}=\dfrac{4}{5}\left(A\right)\)
\(\Rightarrow P_3=I_3^2.R_3=\left(\dfrac{4}{5}\right)^2.10=6,4\left(W\right)\)
\(R_{tđ}=\dfrac{R_{23}.R_1}{R_{23}+R_1}=\dfrac{\left(10+30\right).20}{\left(10+30\right)+20}=\dfrac{40}{3}\left(\Omega\right)\)
Điện năng đoạn mạch tiêu thụ trong 20ph:
\(A=P.t=\dfrac{U^2}{R}.t=\dfrac{24^2}{\dfrac{40}{3}}.20.60=51840\left(J\right)\)
Cảm ơn ạ