cho tam giac ABC nhon co AB<AC, goi M la trung diem cua BC.
a/ so sanh AM va AC
b/ tren tia doi cua tia MA lay diem D sao choMD=MA. chung minh AB=DC
c/chung minh goc BAM>goc CAM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 12 2018
Bài làm
co hinh tam giac co 3 goc nhon : Đ
co hinh tam giac co 3 goc tu : S
co hinh tam giac co 1 goc tu va 2 goc nhon: Đ
co hinh tam giac co 1 goc nhon va 2 goc tu : S
co hinh tam giac co 1 goc vuong va 2 goc nhon : Đ
co hinh tam giac co 1 goc vuong va 2 goc tu : S
# Chúc bạn học tốt #
KV
15 tháng 3 2023
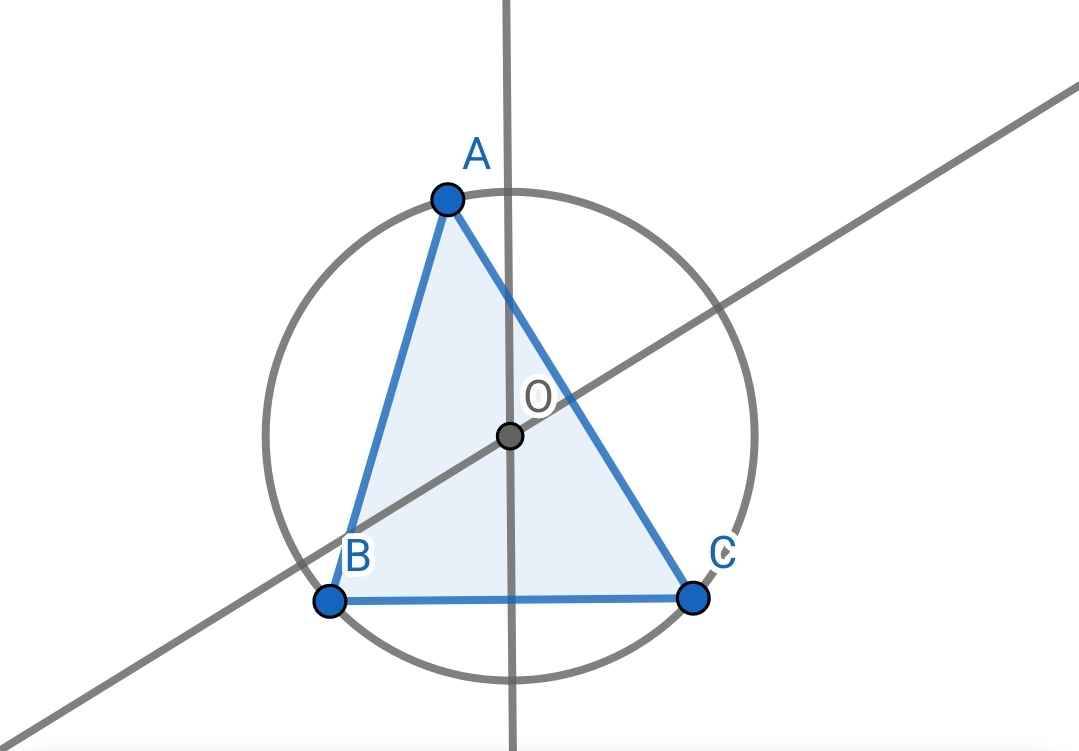
Vẽ hai đường trung trực của hai cạnh của tam giác
Gọi O là giao điểm của chúng
⇒ Tâm của đường tròn ngoại tiếp ∆ABC là O
ND
0
27 tháng 5 2019
kẻ đường cao AH
Ta có: BH=HC=\(\frac{BC}{2}=\frac{c}{2}\)\(\frac{ }{ }\)
theo hệ thức lượng trong tam giác vuông ta có: \(AH^2=BH.HC=>AH=\sqrt{\frac{c}{2}.\frac{c}{2}}=\frac{c^2}{4}\)
diện tích tam giác ABC = \(\frac{1}{2}.AH.BC=\frac{1}{2}.\frac{c^2}{4}.c=\frac{c}{8}\)
vậy diện tích tam giác ABC = \(\frac{c}{8}\)
DT
0
26 tháng 3 2016
1.c/m tam giac ABE đồng dạng với tam giác ACF
xét 2 tam giác ABE va tam giác ACF có
goc AEB=goc AFC
góc A chung
suy ra tam giác ABE đồng dạng với tam giác ACF(g,g)
2.c/m HE.HB=HC.HF
xét 2 tam giác EHC và FHB có
goc HEC=goc HFB
góc EHC=góc FHB(đ đ)
suy ra 2 tam giác EHC đồng dạng với tam giác FHB
nên ta có EH/FH=HC/HB=EC/FB
mà EH/FH=HC/HB suy ra EH.HB=HC.HF(ĐPCM)
cho lời nhân xét nhé
26 tháng 3 2016
1. c/m tam giác ACF đồng dạng tam giác ABE
xét tam giác ACF và tam giác ABE
có góc AEB=góc AFC
góc A chung
suy ra tam giác ACF đồng dạng với tam giác ABE(g.g)
2. c/m HE.HB=HC.HF
Xét 2 tam giác HEC và tam giác HFB
Có góc HEC= góc HFB
góc EHC=góc FHB(đ.đ)
suy ra tam giác HEC đồng dạng với tam giác HFB
Nên ta có HE/HF=HC/HB=EC/FB
Suy ra HE.HB=HF.HC(đpcm)
cho mk lời nhận xét nhé
G
14 tháng 10 2017
Hình vẽ:
Giải:
Xét tam giác ABH và tam giác DBH, ta có:
\(\widehat{AHB}=\widehat{DHB}=90^0\)
\(HA=HD\left(gt\right)\)
HB là cạnh chung
\(\Rightarrow\Delta ABH=\Delta DBH\) (Hai cạnh góc vuông)
Lại xét tam giác ACH và tam giác DCH, ta có:
\(\widehat{AHC}=\widehat{DHC}=90^0\)
\(HA=HD\left(gt\right)\)
HC là cạnh chung
\(\Rightarrow\Delta ACH=\Delta DCH\) (Hai cạnh góc vuông)
Chúc bạn học tốt!