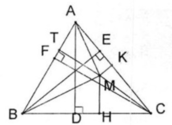
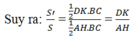Cho tam giác ABC, kẻ 3 đường thẳng AM,BN,CP nằm trong tam giác. G là giao điểm của 03 đường thẳng trên. Chứng minh rằng nếu S tam giác GAC= S tam giác GBC= S tam giác GAB (S là diện tích) thì G là trọng tâm của tam giác.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
24 tháng 3 2018
Em tham khảo tại link này nhé.
Câu hỏi của truong nhat linh - Toán lớp 7 - Học toán với OnlineMath
L
18 tháng 7 2015
Kéo dài BG cắt AC tại N; CG cắt AB tại M
Có : SAGC = \(\frac{1}{2}\)h.GC ; SBGC = \(\frac{1}{2}\). k. GC mà SAGC = SGBC nên h = k
Mặt khác, SGAM = \(\frac{1}{2}\)h.GM ; SGBM = \(\frac{1}{2}\)k. GM
=> SGAM = SGBM
Lại có : tam giác GAM; GBM đều chung chiều cao hạ từ G xuống AB => đáy MA = MB => M là trung điểm của AB => CM là trung tuyến
+) Tương tự, từ SGAB = SGBC => N là trung điểm của AC => BN là trung tuyến
BN cắt CM tại G => G là trọng tâm tam giác ABC
CH
Cô Hoàng Huyền
Admin
VIP
24 tháng 3 2018
Gọi M là giao điểm của GA với BC.
Ta thấy \(S_{GAB}=S_{GAC}\) mà hai tam giác trên chung cạnh đáy GA nên chiều cao hạ từ B và C xuông GA là bằng nhau.
Vậy thì \(S_{GBM}=S_{GCM}\)
Từ đó suy ra BM = CM hay M là trung điểm BC.
Vậy AM là trung tuyến tam giác ABC.
Lại có \(S_{GBM}=\frac{S_{GBC}}{2}=\frac{S_{ABG}}{2}\Rightarrow\frac{AG}{GM}=2\)
Vậy nên G là trọng tâm tam giác ABC.
F
16 tháng 9 2017
Tam giác ABC có đường thẳng d cắt AB tại E và AC tại F
Ta có S(AEF)/S(ABC) = AE.AF/AB.AC
Ghi chú: S(ABC) là diện tích tam giác ABC
Từ AM/AB = BN/BC = CP/CA = 1/3
=> BM/BA = CN/CB = AP/AC = 2/3
Áp dụng ta có:
S(AMP)/S(ABC) = AM.AP/AB.AC = 1/3.2/3 = 2/9 (1)
S((BMN)/S(ABC) = BN.BM/BC.BA = 1/3.2/3 = 2/9 (2)
S(CNP)/S(ABC) = CN.CP/CB.CA = 1/3.2/3 = 2/9 (3)
Cộng (1), (2), (3) vế theo vế ta có:
[S(AMP) + S(BMN) + S(CNP)]/S(ABC) = 6/9 = 2/3
=> S(AMP) + S(BMN) + S(CNP) = 2/3.S(ABC) = 2/3.S
Mà S(AMP) + S(BMN) + S(CNP) + S' = S
=> S' = S - 2/3.S = 1/3.S
CM
18 tháng 4 2017
a) Tam giác AGP và PGB có chung đường cao hạ từ đỉnh G và AP = PB nên SAGP = SPGB
Tương tự, ta có: SBGM = SMGC và SCGN = SNGA.
Vì G là trọng tâm DABC Þ AG = 2GM.
Þ SBGM = 1 2 SABG Þ SBGM = SAGP = SPGB.
Chứng minh tương tự, ta suy ra được:
SAGP = SPGB = SBGM = SMGC = SCGN = SNGA
b) Sử dụng kết quả câu a) ta có diện tích mỗi tam giác bằng 1 6 SABC, từ đó suy ra ĐPCM.
CM
22 tháng 1 2019
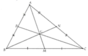
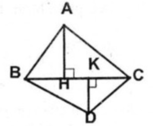
Hai △ ABC và △ DBC có chung canh đáy BC nên ta có:
S A B C = 1/2 AH. BC = S
S D B C = 1/2 DK. BC = S'
