giải câu 12 thôi ( giải chi tiết ra giúp với ) 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LD
2
22 tháng 10 2021
\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
22 tháng 10 2021
a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)
LT
giúp e giải gấp với ạ mấy câu lí thuyết thì ghi đáp án thôi còn mấy câu bài toán thì giải chi tiết ạ
0
7 tháng 5 2022
Câu 4)
Khi vật có khả năng thực hiện công ta nói vật có cơ nănggggg
Đơn vị của cơ năng là J(jun)
Có 2 dạng chính
- Thế năng
+ Quả bóng bay trên trời ( quả bóng ở trên cao + khối lượng quả bóng ---> thế năng )
- Động năng
+ Ô tô đang chạy
+ Ô tô có vận tốc + khối lượng oto --> động năngg
LM
1
8 tháng 9 2023
Peter takes a bus to school every morning. (Peter cầm một chuyến xe buýt đi học mỗi buổi sáng.)
Did you have a little trouble with your car last week? (Bạn đã gặp chút khó khăn với xe hơi của bạn tuần trước chứ?)
I have read that novel by Hemingway several times before. (Tôi đã đọc cuốn tiểu thuyết đó của Hemingway một vài lần trước đây.)
Nam was talking to his mother on the phone at 9 a.m. last night. (Nam đang nói chuyện với mẹ của anh ta qua điện thoại vào 9 giờ tối hôm qua.)
My family lived in Vietnam from 1975 to 1986. (Gia đình tôi sống ở Việt Nam từ năm 1975 đến năm 1986.)
Yesterday the weather was hot. (Hôm qua thời tiết nóng.)
My younger sister has lived in Singapore since 2015. (Em gái tôi đã sống ở Singapore từ năm 2015.)
My father is watching TV in the living room now. (Cha tôi đang xem TV ở phòng khách hiện tại.)
I will be visiting the Sydney Opera House with my parents next month. (Tôi sẽ thăm Nhà hát Opera Sydney cùng bố mẹ của tôi vào tháng tới.)
I have not met Mary since she moved to the United States with her family. (Tôi chưa gặp Mary kể từ khi cô ấy chuyển đến Hoa Kỳ cùng gia đình.)
My mother usually gets up early to prepare breakfast for the whole family. (Mẹ tôi thường thức dậy sớm để chuẩn bị bữa sáng cho cả gia đình.)
My family only got home from France yesterday evening. (Gia đình tôi chỉ mới về nhà từ Pháp vào tối qua.)
Many of my schoolmates were invited to my birthday party last year. (Nhiều bạn cùng trường của tôi đã được mời đến buổi tiệc sinh nhật của tôi năm ngoái.)
Reading books has been my hobby since I was very young. (Đọc sách đã là sở thích của tôi từ khi tôi còn rất nhỏ.)
Mrs. Mai and her friends from Vietnam are planning to attend the festival now. (Bà Mai và những người bạn của bà từ Việt Nam đang lên kế hoạch tham gia lễ hội hiện tại.)
I will give you a book when I visit you tomorrow. (Tôi sẽ tặng bạn một quyển sách khi tôi đến thăm bạn ngày mai.)
When I met Peter at the supermarket yesterday, he was doing shopping with his friends. (Khi tôi gặp Peter tại siêu thị hôm qua, anh ta đang mua sắm cùng bạn bè của mình.)
Before Mary visited Vietnam, she had spent a lot of time learning Vietnamese. (Trước khi Mary đến thăm Việt Nam, cô ấy đã dành rất nhiều thời gian để học tiếng Việt.)
I think you should spend as much time as possible doing your homework. (Tôi nghĩ bạn nên dành càng nhiều thời gian càng tốt để làm bài tập về nhà của bạn.)
TT
1
TN
1
LT
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
23.
Ta sẽ tìm điểm \(I\left(a;b;c\right)\) sao cho \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\) (1)
\(\left\{{}\begin{matrix}\overrightarrow{IA}=\left(-2-a;2-b;6-c\right)\\\overrightarrow{IB}=\left(-3-a;1-b;8-c\right)\\\overrightarrow{IC}=\left(-1-a;-b;7-c\right)\\\overrightarrow{ID}=\left(1-a;2-b;3-c\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\left(-5-4a;5-4b;24-4c\right)\)
(1) thỏa mãn khi: \(\left\{{}\begin{matrix}-5-4a=0\\5-4b=0\\24-4c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{4}\\b=\dfrac{5}{4}\\c=6\end{matrix}\right.\)
\(\Rightarrow I\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\)
Khi đó:
\(T=MA^2+MB^2+MC^2+MD^2=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{ID}\right)^2\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2+2\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}\right)\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2\) (do \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\))
\(IA^2+IB^2+IC^2+ID^2\) cố định nên \(T_{min}\) khi \(MI_{min}\)
\(\Leftrightarrow M\) trùng I
\(\Rightarrow M\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\Rightarrow x+y+z=-\dfrac{5}{4}+\dfrac{5}{4}+6=6\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
24.
\(a+b=4\Rightarrow b=4-a\)
ABCD là hình chữ nhật \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow C\left(a;a;0\right)\)
Tương tự ta có: \(C'\left(a;a;b\right)\)
M là trung điểm CC' \(\Rightarrow M\left(a;a;\dfrac{b}{2}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{A'B}=\left(a;0;-b\right)=\left(a;0;a-4\right)\\\overrightarrow{A'D}=\left(0;a;-b\right)=\left(0;a;a-4\right)\\\overrightarrow{A'M}=\left(a;a;-\dfrac{b}{2}\right)=\left(a;a;\dfrac{a-4}{2}\right)\end{matrix}\right.\)
Theo công thức tích có hướng:
\(\left[\overrightarrow{A'B};\overrightarrow{A'D}\right]=\left(-a^2+4a;-a^2+4a;a^2\right)\)
\(\Rightarrow V=\dfrac{1}{6}\left|\left[\overrightarrow{A'B};\overrightarrow{A'D}\right].\overrightarrow{A'M}\right|=\dfrac{1}{6}\left|a\left(-a^2+4a\right)+a\left(-a^2+4a\right)+\dfrac{a^2\left(a-4\right)}{2}\right|\)
\(=\dfrac{1}{4}\left|a^3-4a^2\right|=\dfrac{1}{4}\left(4a^2-a^3\right)\)
Xét hàm \(f\left(a\right)=\dfrac{1}{4}\left(4a^2-a^3\right)\) trên \(\left(0;4\right)\)
\(f'\left(a\right)=\dfrac{1}{4}\left(8a-3a^2\right)=0\Rightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=\dfrac{8}{3}\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)_{max}=f\left(\dfrac{8}{3}\right)=\dfrac{64}{27}\)
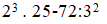
\(\dfrac{l_1}{l_2}=\dfrac{R.S}{\rho_1}:\dfrac{R.S}{\rho_2}=\dfrac{\rho_2}{\rho_1}\Rightarrow l_2=\dfrac{l_1.\rho_1}{\rho_2}=\dfrac{2.1,7.10^{-8}}{1,1.10^{-6}}\approx0,03m\approx3cm\Rightarrow A\)
lên đc Cộng tác viên rồi hả :))