Giải phương trình;\(m\left(2x-m\right)\ge2\left(x-m\right)+1\)Với m là tham số.
Với a,b,c là số dương. Chứng minh
a) \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
b)\(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\ge\frac{3}{2}\)



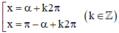
 ta được:
ta được:

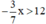 . Ta có:
. Ta có: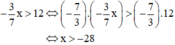
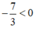 mà không đổi chiều bất phương trình.
mà không đổi chiều bất phương trình.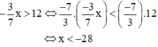
\(1.\) Giải phương trình
\(m\left(2x-x\right)\ge2\left(x-m\right)+1\)
Biến đổi tương đương!
\(\Leftrightarrow\) \(2mx-mx\ge2x-2m+1\)
\(\Leftrightarrow\) \(2mx-mx-2x\ge-2m+1\)
\(\Leftrightarrow\) \(x\left(m-2\right)\ge-2m+1\) \(\left(\text{*}\right)\)
\(a.\) Nếu \(m>2\) thì nghiệm của bất phương trình có dạng \(x\ge\frac{1-2m}{m-2}\)
\(b.\) Nếu \(m<2\) thì nghiệm của bất phương trình có dạng \(x\le\frac{1-2m}{m-2}\)
\(c.\) Nếu \(m=2\) thì \(\left(\text{*}\right)\) có dạng \(0x\ge-3\), nghiệm của bất phương luôn đúng với mọi \(x\)
\(2.\) Áp dụng bđt Cauchy cho 3 số dương a,b,c là ra