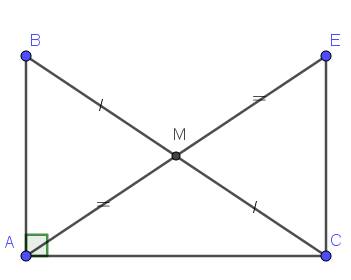
cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Trên tia đối của tia MA lây điểm E sao cho ME = MA a. Tính số đo của góc ACB khi goac ACB = 40 độb. C/m : tam giác AMB = tam giác EMC và AB so...

ND

Nga Dayy

25 tháng 12 2021

cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Trên tia đối của tia MA lây điểm E sao cho ME = MA a. Tính số đo của góc ACB khi goac ACB = 40 độb. C/m : tam giác AMB = tam giác EMC và AB song song EC c. Từ C kẻ đường thẳng (d) song song với AE. Kẻ EK vuông góc với đường thẳng (d) tại K. Chừng minh góc KEC = góc BCAgiúp...

Đọc tiếp

#Toán lớp 7

0

ND

nguyễn đăng khánh

24 tháng 12 2021

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.a) Tính số đo của góc ABC khi góc ACB=40 độb) Chứng minh: tam giác AMB = tam giác EMC và AB // EC.c) Từ C kẻ đường thẳng (d) song song với AE. Kẻ EK vuông góc đường thẳng (d) tại K. Chứng minh: góc KEC= góc...

Đọc tiếp

#Toán lớp 7

0

T1

TiTan . 19 Móng Qủy

10 tháng 1 2021

cho tam giác abc vuông cân tại a m là trung điểm của bc . Gọi M là trung điểm của BC . Trên tia đới của tia MA lấy điểm E sao cho ME= MA

a,tính số đo của góc ABC khi góc ACB=40 độ.

b,chứng minh tam giác AMB = EMC và AB//EC

c,từ C kẻ đường thẳng song song với AE. Kẻ EK vuông góc đường thẳng tại K.Chứng minh: góc KEC =BCA

#Toán lớp 7

1

TT

Thu Thao

10 tháng 1 2021

Bạn gõ thừa chữ "cân"

a/ Xét t/g ABC vuông tại A có

$\widehat{ABC}+\widehat{ACB}=90^o$ (t/c)

$\Rightarrow\widehat{ABC}=90^o-40^o=50^o$

b/ Xét t/g AMB và t/g EMC có

AM = EM

$\widehat{AMB}=\widehat{EMC}$ (đối đỉnh)MB = MC

=> t/g AMB = t/g EMC (c.g.c)c/ Có

AE // CK

=> $\widehat{AEK}+\widehat{EKC}=180^o$ (tcp)

=> $\widehat{AEK}=\widehat{AEC}+\widehat{CEK}=90^o$

Xét t/g ABC vuông tại A có AM là đường trung tuyến

=> AM = 1/2 BC = BM

=> t/g AMB cân tại A

=> $\widehat{ABC}=\widehat{BAM}$

Mà $\widehat{BAM}=\widehat{CEA}$

=> $\widehat{CBA}+\widehat{CEK}=90^o$

=> $\widehat{CEK}=\widehat{ACB}$

Đúng(3)

TT

Trần Thị Huyền Thanh

21 tháng 2 2019 - olm

cho tam giác ABC vuông tại A. gọi M là trung điểm của BC. Trên tia đối của tia MA lấy E sao cho ME = MA

a) tính số đo góc ABC khi góc ACB = 60 độ

b) tam giác AMB= tam giác EMC và AB // EC

c) từ C kẻ đường thẳng 9 (d) song song với AE. kẻ EK song song với đường thẳng (d) tại K. chứng minh góc KEC = góc BCA

#Toán lớp 7

1

NL

Nguyễn Linh Chi

11 tháng 12 2019

Câu hỏi của le thu giang - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo bài làm tương tự ở link trên.

Đúng(0)

ND

Nguyễn Đức Anh

19 tháng 12 2015 - olm

cho tam giác ABC vuông tại A Gọi M là trung điểm của BC Trên tia đối tia MA lấy điểm E sao cho MA=ME

a, tính số đo của <ABC khi <ACB = 40độ

b, chứng minh tam giác AMB = tam giác EMC và AB // EC

c, từ C kẻ đường thẳng ( d ) song song với AE Kẻ EK vuông góc đường thẳng ( d) tại K Chứng minh rằng

<KEC = <BCA

#Toán lớp 8

0

PH

Park Hye Young

14 tháng 2 2016 - olm

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.

a) Tính số đo của góc ABC khi góc ACB = 40độ.

b) Chứng minh tam giác AMB = EMC và AB // EC.

c) Từ C kẻ đường thẳng d song song với AE. Kẻ EK vuông góc đường thẳng d tại K . Chứng minh: góc KEC = BCA

Giup mình giải nhanh bài này với nha!

#Toán lớp 6

0

PG

Phương Genz TThị

31 tháng 12 2022

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.a) Tính số đo của góc ABC khi góc ACB = 40 độ.b) Chứng minh: ΔAMB = ΔEMC và AB // EC.c) Từ C kẻ đường thẳng (d) song song với AE. Kẻ EK vuông góc đường thẳng (d) tại K. Chứng minh: góc KEC = góc BCA.NHỚ KẺ HÌNH NHA MIK CẢM...

Đọc tiếp

#Toán lớp 7

1

NT

Ng Thùy Linh

31 tháng 12 2022

Lười quá ko mún kẻ= thước =))) loading...

Đúng(1)

GL

Giáp Lê Mai Linh

25 tháng 12 2022 - olm

cho tam giác ABC vuông tại A. gọi M là trung điểm của BC. trên tia đối của tia MA lấy điểm E sao cho ME= MA. Chứng Minh rằng rằng:

a, tam giác AMB = tam giác EMC

b, AC vuông góc với CE

c, BC = 2.AM

#Toán lớp 7

2

AH

Akai Haruma

Giáo viên

26 tháng 12 2022

Lời giải:
a.

Xét tam giác $AMB$ và $EMC$ có:

$\widehat{AMB}=\widehat{EMC}$ (đối đỉnh)

$AM=EM$

$MB=MC$

$\Rightarrow \triangle AMB=\triangle EMC$ (c.g.c)

b.

Vì $\triangle AMB=\triangle EMC$ nên $\widehat{MAB}=\widehat{MEC}$

Mà 2 góc này ở vị trí so le trong nên $EC\parallel AB$

Mà $AB\perp AC$ nên $EC\perp AC$ (đpcm)

c.

Vì $\triangle AMB=\triangle EMC$ nên:

$AB=EC$

Vì $EC\perp AC$ nên $\widehat{ECA}=90^0=\widehat{BAC}$

Xét tam giác $ECA$ và $BAC$ có:
$\widehat{ECA}=\widehat{BAC}=90^0$ (cmt)

$AC$ chung

$EC=BA$ (cmt)

$\Rightarrow \triangle ECA=\triangle BAC$ (c.g.c)

$\Rightarrow EA=BC$

Mà $EA=2AM$ nên $2AM=BC$ (đpcm)

Đúng(0)

AH

Akai Haruma

Giáo viên

26 tháng 12 2022

Hình vẽ:

Đúng(1)

TH

Trag Hòag

13 tháng 12 2015 - olm

Cho tam giác ABC vuông ở A. Gọi M là trung điểm của BC. Trên tia đối MA lấy điểm E sao cho ME = MA.

a. Tính số đo góc C khi góc B = 40 độ

b. Chứng minh tam giác AMB = tam giác EMC

c. Chứng minh AB // EC

d. Từ C kẻ D // AE. Kẻ EK vuông góc ở D tại A. Chứng minh rằng : GÓc KEC = góc BCA

#Toán lớp 7

0

JJ

Jungkook Jeon

13 tháng 1 2021 - olm

Cho tam giác ABC vuông tại A, gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME=MA.a) Tính số đo của góc ABC biết số đo của góc ACB là 40 độ.b) Chứng minh rằng: tam giác AMB= tam giác EMC và AB//ECc) Từ C kẻ đường thẳng d//AE. Kẻ EK vuông góc với d tại K. Chứng minh góc KEC = góc BCAMọi Người Giúp Em Với Ạ. Nếu Được Cho Em Xin Hình Vẽ Luôn Ạ.Em...

Đọc tiếp

#Toán lớp 7

1

.

13 tháng 1 2021

Giải:

Làm phiền bạn tự vẽ hình ạ. :(((

a) Ta có: tam giác ABC vuông tại A (gt)

=> Góc ABC + góc ACB = 90^o (định lí)

=> Góc ABC = 90^o - góc ACB = 90^o - 40^o = 50^o

Vậy góc ACB = 50^o.

b) Vì M là trung điểm của BC (gt)

nên BM = CM

Xét tam giác ABM và tam giác CEM có:

BM = CM (chứng minh trên)

Góc AMB = góc CME (2 góc đối đỉnh)

AM = EM (gt)

=> Tam giác ABM = tam giác ECM (c.g.c) (đpcm)

c) Ta có: tam giác ABM = tam giác ECM (chứng minh trên)

=> Góc BAM = góc CEM (2 góc tương ứng)

Mà 2 góc này ở vị trí so le trong

=> AB // CE (dấu hiệu nhận biết)

Lại có: AE // d (gt), EK _|_ d tại K (gt)

=> EK _|_ AE tại E

=> Góc AEK = 90^o

hay góc AEC + góc CEK = 90^o

Xét tam giác ABC và tam giác ACE có:

AB = CE (vì tam giác ABC = tam giác ECM)

Góc BAC = góc ACE (= 90^o)

AC là cạnh chung

=> Tam giác ABC = tam giác CEA (c.g.c)

=> Góc ABC = góc AEC (2 góc tương ứng)

Mà góc AEC + góc CEK = 90^o (chứng minh trên)

góc ABC + góc ACB = 90^o (chứng minh trên)

=> Góc CEK = góc ACB (đpcm)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP