Mọi người giúp em câu 7b với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DY
2
8 tháng 6 2021
Bạn tự vẽ hình nhé!
Vì AC và MC là 2 tt cắt tại C
`=>OC` là phân giác `hat{AOM}`
`=>hat{COM}=hat{COA}=1/2hat{AOM}`
Tương tự do MD và BD là 2 tt cắt tại D
`=>hat{MOD}=1/2hat{BOM}`
`=>hat{COM}+hat{DOM}=1/2(hat{AOM}+hat{BOM})=1/2*180^o=90^o`
Hay `hat{COD}=90^o`
AT
8 tháng 6 2021
Vì CM,CA là tiếp tuyến \(\Rightarrow OC\) là phân giác \(\angle MOA\)
\(\Rightarrow\angle MOA=2\angle MOC\)
Vì DM,DB là tiếp tuyến \(\Rightarrow OD\) là phân giác \(\angle MOB\)
\(\Rightarrow\angle MOB=2\angle MOD\)
\(\Rightarrow\angle COD=\angle MOD+\angle MOC=\dfrac{1}{2}\left(\angle MOB+\angle MOA\right)=\dfrac{1}{2}\angle AOB\)
\(=\dfrac{1}{2}.180=90\)
còn khúc sau chắc bạn tự giải quyết được rồi nhỉ
30 tháng 11 2021
Câu 92:
\(a,PTHH:Zn+2HCl\to ZnCl_2+H_2\\ ZnO+2HCl\to ZnCl_2+H_2O\\ n_{H_2}=\dfrac{2,24}{22,4}=0,1(mol)\\ \Rightarrow n_{Zn}=0,1(mol)\\ \Rightarrow m_{Zn}=0,1.65=6,5(g)\\ \Rightarrow \%_{Zn}=\dfrac{6,5}{14,6}.100\%\approx44,52\%\\ \Rightarrow \%_{ZnO}=100\%-44,52\%=55,48\%\\ b,m_{ZnO}=14,6-6,5=8,1(g)\\ \Rightarrow n_{ZnO}=\dfrac{8,1}{81}=0,1(mol)\\ \Rightarrow \Sigma n_{HCl}=2n_{Zn}+2n_{ZnO}=0,4(mol)\\ \Rightarrow V_{dd_{HCl}}=\dfrac{0,4}{0,5}=0,8(mol)\)
30 tháng 11 2021
Câu 93:
\(n_{H_2}=\dfrac{16,8}{22,4}=0,75(mol)\\ PTHH:Fe+H_2SO_4\to FeSO_4+H_2\\ \Rightarrow n_{Fe}=n_{H_2}=0,75(mol)\\ \Rightarrow m_{Fe}=0,75.56=42(g)\\ b,n_{H_2SO_4}=n_{H_2}=0,75(mol)\\ \Rightarrow C_{M_{H_2SO_4}}=\dfrac{0,75}{0,25}=3M\\ c,n_{FeSO_4}=0,75(mol)\\ \Rightarrow m_{CT_{FeSO_4}}=0,75.152=114(g)\\ V_{dd_{FeSO_4}}=V_{dd_{H_2SO_4}}=250(ml)\\ \Rightarrow m_{dd_{FeSO_4}}=250.1,1=275(g)\\ \Rightarrow C\%_{FeSO_4}=\dfrac{114}{275}.100\%\approx41,45\%\)
\(d,m_{FeSO_4.5H_2O}=242.0,75=181,5(g)\)
TA
1
MT
2
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
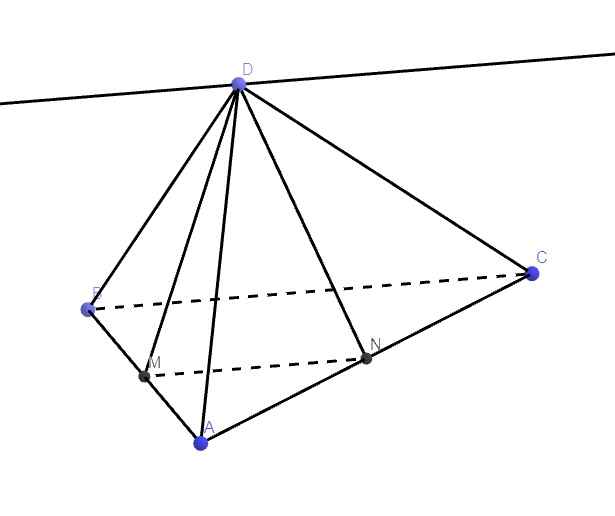
Giả thiết suy ra MN là đường trung bình tam giác ABC \(\Rightarrow MN||BC\)
Mà \(\left\{{}\begin{matrix}MN=\left(DMN\right)\cap\left(ABC\right)\\BC=\left(BCD\right)\cap\left(ABC\right)\end{matrix}\right.\)
Và D là 1 điểm chung của (BCD) và (DMN)
\(\Rightarrow\) Giao tuyến của (BCD) và (DMN) phải là 1 đường thẳng qua D và song song MN (hoặc BC)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
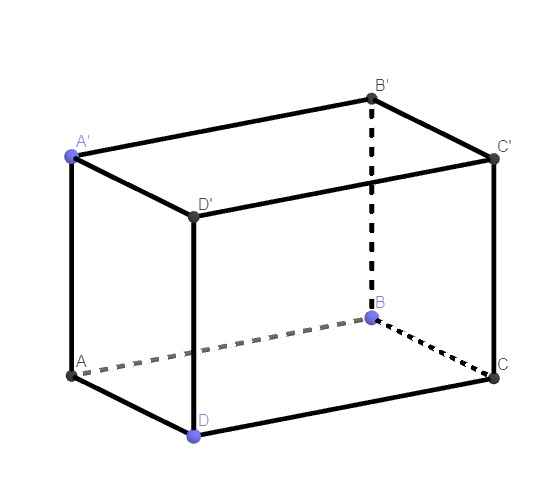
71.
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)
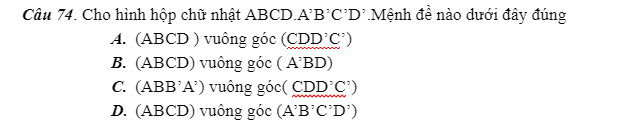
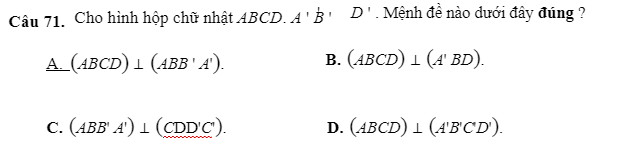
Chứng minh: Tam giác ABK đồng dạng với tam giác ADB
=> \(AB^2=AK.AD\)
Mà Tam giác ABO vuông tại B có BH là đg cao
\(\Rightarrow AB^2=AH.AO\)
=> AK.AD = AH.AO