Chob>a>0 thỏa mãn:2a2+2b2=5ab Khi đó giá trị của biểu thức:2b/a-b +1 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 3 2016
Có: 2a2 + 2b2 = 5ab => 2(a2 + b2) = 5ab => a2 + b2 = \(\frac{5}{2}\)ab
\(A=\frac{2b}{a-b}+1=\frac{2b+a-b}{a-b}=\frac{a+b}{a-b}=\frac{\left(a+b\right)^2}{\left(a-b\right)^2}=\frac{a^2+b^2+2ab}{a^2+b^2-2ab}=\frac{\frac{5}{2}ab+2ab}{\frac{5}{2}ab-2ab}=\frac{\frac{9}{2}ab}{\frac{1}{2}ab}=9\)
Vậy A = 9
TN
29 tháng 6 2016
\(a^3-a^2b+ab^2-6b^3=0\)
\(\Leftrightarrow\left(a-2b\right)\left(a^2+ab+3b^2\right)=0\left(1\right)\)
Vì a>b>0 =>a2+ab+3b2>0 nên từ (1) ta có a=2b
Vậy biểu thức \(A=\frac{a^4-4b^4}{b^4-4a^4}=\frac{16b^4-4b^4}{b^4-64b^4}=\frac{12b^4}{-63b^4}=-\frac{4}{21}\)
KT
7 tháng 11 2018
\(2a^2+2b^2=5ab\)
<=> \(2a^2+2b^2-5ab=0\)
<=> \(2a^2-4ab-ab+2b^2=0\)
<=> \(2a\left(a-2b\right)-b\left(a-2b\right)=0\)
<=> \(\orbr{\begin{cases}2a=b\\a=2b\end{cases}}\)
Do b > a > 0
=> b = 2a
\(A=\frac{a+b}{a-b}=\frac{a+2a}{a-2a}=\frac{3a}{-a}=-3\)
KT
7 tháng 11 2018
\(2a^2+2b^2=5ab\)
<=> \(2a^2+2b^2-5ab=0\)
<=> \(2a^2-4ab-ab+2b^2=0\)
<=> \(2a\left(a-2b\right)-b\left(a-2b\right)=0\)
<=> \(\left(2a-b\right)\left(a-2b\right)=0\)
<=> \(\orbr{\begin{cases}2a-b=0\left(L\right)\\a-2b=0\end{cases}}\)
=> \(a=2b\)
=> \(A=\frac{a+2b}{2a-b}=\frac{2b+2b}{2.2b-b}=\frac{4b}{3b}=\frac{4}{3}\)
14 tháng 5 2016
M = 2(a-2ab+b) / 2(a+2ab+b) =ab/9ab = 1/9
lưu ý: a;b binh phuong nhé tui làm bieng viêt
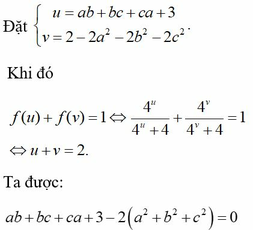
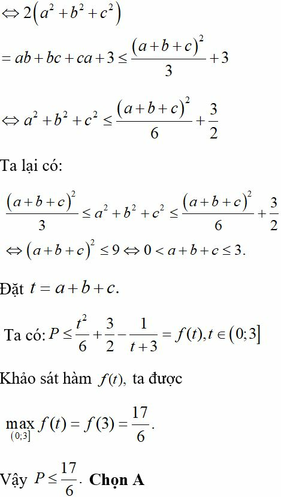
bị nhầm xin lỗi
\(\Rightarrow\left(a+b\right)^2=\frac{9ab}{2};\left(a-b\right)^2=\frac{ab}{2}\)
Suy ra: \(\frac{2b}{a-b}+1=\frac{a+b}{a-b}=\frac{\frac{9ab}{2}}{\frac{ab}{2}}=9\)