Số nghiệm của phương trình: 6 là...
Đọc tiếp
Số nghiệm của phương trình:
6 là ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 9 2023
Tham khảo:
a) Vì \(0 - 2.0 + 6 = 6 > 0\) nên (0;0) là một nghiệm của bất phương trình đã cho.
b) Vì \(0 - 2.1 + 6 = 4 > 0\) nên (0;1) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.0 + 6 = 7 > 0\) nên (1;0) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.1 + 6 = 5 > 0\) nên (1;1) là một nghiệm của bất phương trình đã cho.
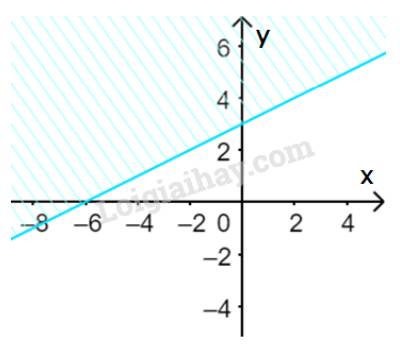
c) Vẽ đường thẳng \(\Delta :x - 2y + 6 = 0\) đi qua hai điểm \(A(0;3)\) và \(B\left( { - 2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 2.0 + 6 = 6 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
.
20 tháng 6 2023
a: a*c<0
=>(1) có hai nghiệm phân biệt
b: Bạn viết lại biểu thức đi bạn
CM
3 tháng 4 2019
Chọn D.
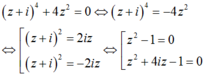
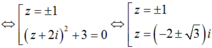
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
PT
1
CM
19 tháng 12 2018
Đáp án C
ĐK x > 6 1 ⇒ x 2 − 6 x = 7 ⇔ x = − 1 l o a i ; x = 7 t m . PT có 1 nghiệm.
25 tháng 1 2023
a: Thay x=-1 vào (6), ta được:
1+2m+m+6=0
=>3m+7=0
=>m=-7/3
x1+x2=-2m/1=-2*7/3=-14/3
=>x2=-14/3-x1=-14/3+1=-11/3
b: \(\text{Δ}=0^2-2\left(2m+m+6\right)=-2\left(3m+6\right)\)
Để phương trình có nghiệm kép thì 3m+6=0
=>m=-2
Khi m=-2 thì (6) sẽ là x^2+2*(-2)-2+6=0
=>x^2-4x+4=0
=>x=2
29 tháng 1 2023
ụa bạn ơi, trên câu a á m= -7/3 vậy sao xuống dưới thành 7/3 rồi
16 tháng 5 2021
`a)ac=-3<0`
`=>b^2-4ac>0`
`=>` phương trình luôn có hai nghiệm phân biệt với mọi m
`b)` áp dụng vi-ét:`x_1+x_2=m,x_1.x_2=-3`
`(x_1+6).(x_2+6) = 2019`
`<=>x_1.x_2+6(x_1+x_2)+36=2019`
`<=>6m-3+36=2019`
`<=>6m+33=2019`
`<=>6m=1986`
`<=>m=331`
Vậy `m=331` thì `(x_1+6).(x_2+6) = 2019`
16 tháng 5 2021
`a)ac=-3<0`
`=>b^2-4ac>0`
`=>` phương trình luôn có hai nghiệm phân biệt với mọi m
`b)` áp dụng vi-ét:`x_1+x_2=m,x_1.x_2=-3`
`(x_1+6).(x_2+6) = 2019`
`<=>x_1.x_2+6(x_1+x_2)+36=2019`
`<=>6m-3+36=2019`
`<=>6m+33=2019`
`<=>6m=1986`
`<=>m=331`
Vậy `m=331` thì `(x_1+6).(x_2+6) = 2019`
16 tháng 5 2021
a,ta có \(\Delta\)=\(\left(-m\right)^2-4.\left(-3\right)=m^2+12\)
vì \(m^2\ge\)0(\(\forall\)m)=>\(m^2+12\ge12=>m^2+12>0=>\Delta>0\)
vậy pt luôn có 2 nghiệm phân biệt với mọi m
b, theo vi ét=>\(\left\{{}\begin{matrix}x1+x2=m\\x1.x2=-3\end{matrix}\right.\)
có \(\left(x1+6\right).\left(x2+6\right)=2019< =>x1.x2+6x1+6x2+36-2019=0< =>-3+6\left(x1.x2\right)-1983=0< =>6m=1986< =>m=\dfrac{1986}{6}=331\)
PT
1
Đề hiển thị lỗi. Bạn xem lại nhé.