TRUI UI HELP TUII (lam on viet chi tiet nhaa)
Cho góc xOy khác góc bẹt, trên Ox, Oy lần lượt lấy hai điểm A, B sao cho OA = OB kẻ các đường thẳng vuông góc với Ox tại A, vuông góc với Oy tại B, hai đường thẳng này cắt nhau tại C.
a. Chứng minh rằng OC là tia phân giác của góc xOy.
b. Gọi I là điểm bất kỳ thuộc tia OC. Gọi M, N theo thứ tự là chân các đường vuông góc kẻ từ I đến Ox, Oy. Chứng minh rằng IM = IN.



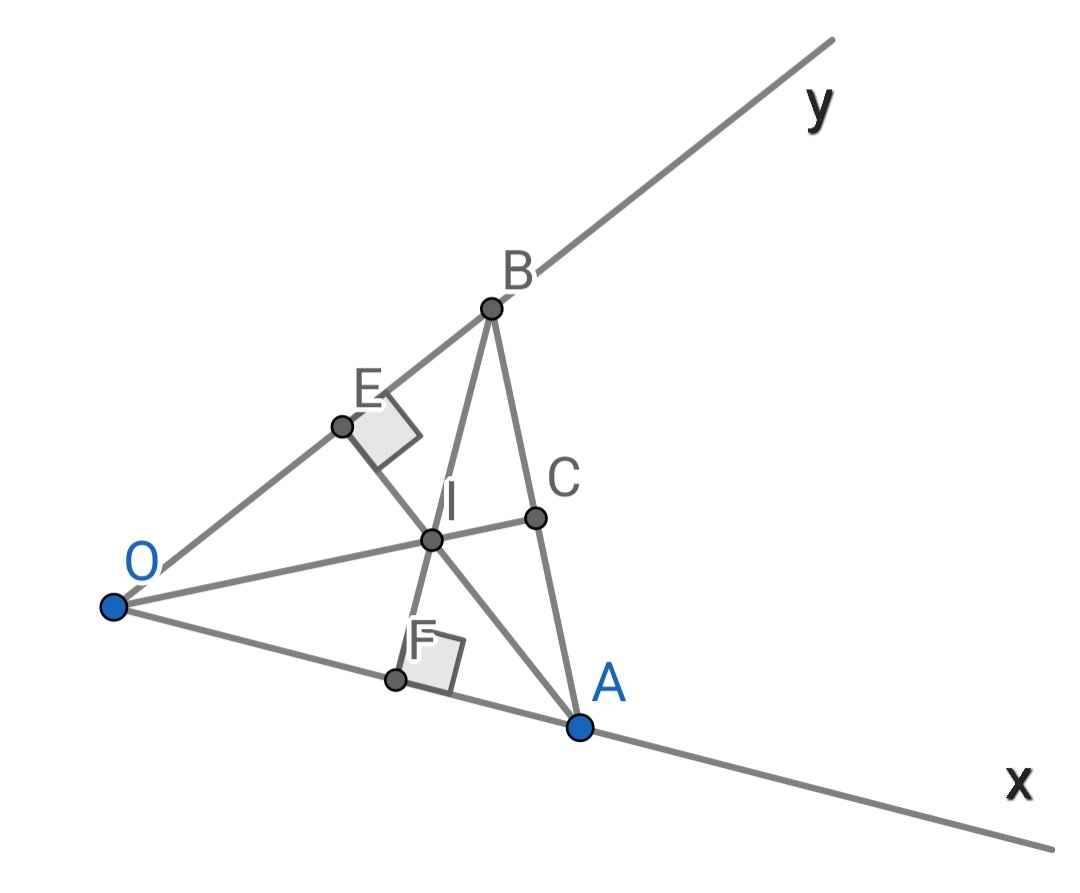


a) Xét ΔOBC và ΔBAC ta có:
∠CBO = ∠CAO = 90o
OA = OB
Cạnh OC chung
=> ΔCBO = ΔCAO (ch-cgv)
=> ∠BCO = ∠ACO => OC là phân giác ∠xOy
và ∠ION = ∠IOM
Xét ΔINO và ΔIMO có:
∠ION = ∠IOM
Cạnh IO chung
∠INO = ∠IMO = 90o
=> ΔINO = ΔIMO (ch-gn)
=> IM = IN