(x + 1) . (6 - 3x) = 0 Giải chi tiết được ko ạ ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\dfrac{3x+2}{6}-\dfrac{3x-2}{4}=\dfrac{15}{8}\\ \Leftrightarrow\dfrac{4\left(3x+2\right)}{24}-\dfrac{6\left(3x-2\right)}{24}-\dfrac{45}{24}=0\\ \Leftrightarrow12x+24-18x+12-45=0\\ \Leftrightarrow-6x-9=0\\ \Leftrightarrow x=-\dfrac{3}{2}\)
2, ĐKXĐ:\(x\ne\pm3\)
\(\dfrac{x+2}{3+x}-\dfrac{x}{3-x}=\dfrac{8x-6}{9-x^2}\\ \Leftrightarrow\dfrac{\left(x+2\right)\left(3-x\right)}{\left(3+x\right)\left(3-x\right)}-\dfrac{x\left(3+x\right)}{\left(3+x\right)\left(3-x\right)}-\dfrac{8x-6}{\left(3+x\right)\left(3-x\right)}=0\\ \Leftrightarrow\dfrac{-x^2+x+6-3x-x^2-8x+6}{\left(3+x\right)\left(3-x\right)}=0\\ \Leftrightarrow-2x^2-10x+12=0\\ \Leftrightarrow x^2+5x-6=0\\ \Leftrightarrow\left(x-1\right)\left(x+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-6\left(tm\right)\end{matrix}\right.\)
\(a,\dfrac{3x+2}{6}-\dfrac{3x-2}{4}=\dfrac{15}{8}\)
\(\Leftrightarrow4\left(3x+2\right)-6\left(3x-2\right)=45\)
\(\Leftrightarrow12x+8-18x+12=45\)
\(\Leftrightarrow12x-18x=45-12-8\)
\(\Leftrightarrow-6x=25\)
\(\Leftrightarrow x=\dfrac{-25}{6}\)
Vậy \(S=\left\{\dfrac{-25}{6}\right\}\)
\(b,\dfrac{x+2}{3+x}-\dfrac{x}{3-x}=\dfrac{8x-6}{9-x^2}\left(ĐKXĐ:x\ne3;x\ne-3\right)\)
\(\Leftrightarrow\left(x+2\right)\left(3-x\right)-x\left(3+x\right)=8x-6\)
\(\Leftrightarrow3x-x^2+6-2x-3x-x^2=8x-6\)
\(\Leftrightarrow-x^2-x^2+3x-2x-3x-8x=-6+6\)
\(\Leftrightarrow-2x^2-10x=0\)
\(\Leftrightarrow-2x\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=5\left(nhận\right)\end{matrix}\right.\)
Vậy \(S=\left\{0;5\right\}\)

Để biểu thức đề bài cho có giá trị nguyên thì \(5\sqrt{x}-6⋮2\sqrt{x}-3\)
\(\Leftrightarrow10\sqrt{x}-12⋮2\sqrt{x}-3\)
\(\Leftrightarrow2\sqrt{x}-3\in\left\{-3;-1;1;3\right\}\)
\(\Leftrightarrow2\sqrt{x}\in\left\{0;2;4;6\right\}\)
hay \(x\in\left\{0;1;4;9\right\}\)


\(\dfrac{1}{x-3}+\dfrac{3x^2-8x+10}{x^2-5x+6}-\dfrac{2x-4}{x-2}\left(ĐK:x\ne3;x\ne2\right)\)
\(=\dfrac{1}{x-3}+\dfrac{3x^2-8x+10}{x\left(x-2\right)-3\left(x-2\right)}-\dfrac{2x-4}{x-2}\)
\(=\dfrac{1}{x-3}+\dfrac{3x^2-8x+10}{\left(x-3\right)\left(x-2\right)}-\dfrac{2x-4}{x-2}\)
\(=\dfrac{x-2}{\left(x-2\right)\left(x-3\right)}+\dfrac{3x^2-8x+10}{\left(x-3\right)\left(x-2\right)}-\dfrac{\left(2x-4\right)\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x-2+3x^2-8x+10-\left(2x^2-6x-4x+12\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{3x^2-7x+8-2x^2+10x-12}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x^2+3x-4}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x^2+3x-4}{x^2-5x+6}\)


Đk: \(x\ge1\)
\(\Leftrightarrow4\left(2\sqrt{x-1}-1\right)+\left(4x-5\right)\left(x+2\right)=0\)
\(\Leftrightarrow\dfrac{4\left(4x-5\right)}{2\sqrt{x-1}+1}+\left(4x-5\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left(4x-5\right)\left(\dfrac{4}{2\sqrt{x-1}+1}+x+2\right)=0\)
\(\Leftrightarrow x=\dfrac{5}{4}\)(Dễ thấy ngoặc to lớn hơn 0 với \(x\ge1\))
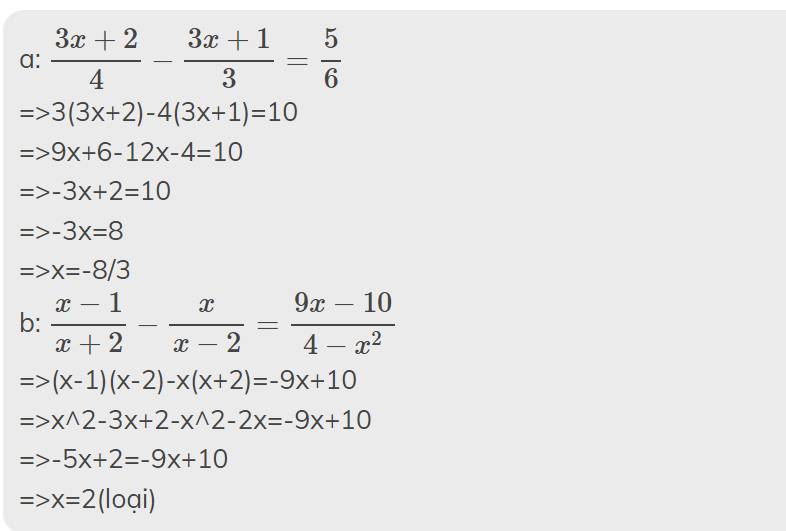
\(x\in\left\{-1;2\right\}\)
\(\left[{}\begin{matrix}x+1=0\\6-3x=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\left(-1\right)\\x=2\end{matrix}\right.\)