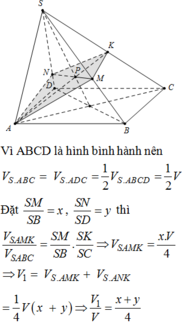
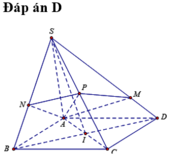
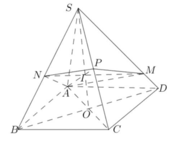
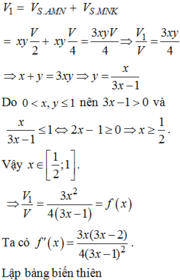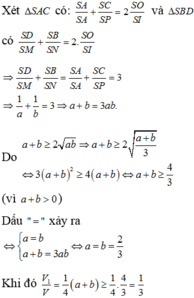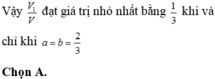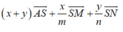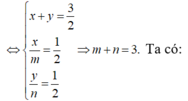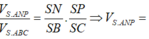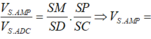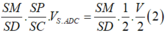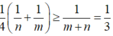Cho khối chóp S.ABCD có đáy là hình bình hành, có thể tích bằng a3. Gọi E là trung điểm SC. Một mặt phẳng chứa AE cắt các cạnh SB và SD lần lượt tại M và N. Tìm giá trị nhỏ nhất của thể tích khối chóp S.AMEN.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 10 2018
Đáp án C
Giả sử S D → = m . S M → ; S B → = n . S N → .
S A → + S C → = S B → + S D →
Do A; M; N; K đồng phẳng nên m + n = 3 .
V S . A K M V S . A B C = 1 2 .1. 1 m = 1 2 m ⇒ V S . A K M V = 1 4 m
Tương tự ta có V S . A K N V = 1 4 n ⇒ V ' V = 1 4 . m + n m n = 3 4 m n ≥ 3 m + n 2 = 3 3 2 = 1 3 .
Dấu bằng xảy ra khi m = n = 1,5 .
CM
20 tháng 11 2017
Phương pháp:
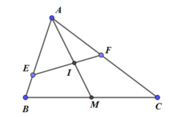
∆ ABC có AM là trung tuyến, I là điểm bất kì trên đoạn AM, đường thẳng đi qua I cắt AB, AC lần lượt tại E, F.
Khi đó: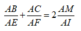 
Cách giải:
Ta có: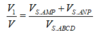
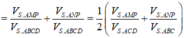
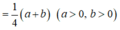
Xét
∆
SAC có: 
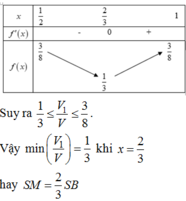
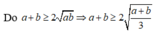
Dấu "=" xảy ra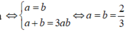 
Khi đó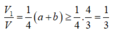 
Vậy V 1 V đạt giá trị nhỏ nhất bằng 1 3 khi và chỉ khi a= b = 2 3
Chọn A.
CM
13 tháng 1 2017
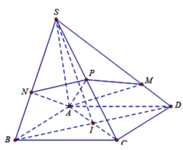
Giả sử S D → = m S M → , S B → = n S N →
Ta có S A → + S C → = S B → + S D → = 2 S I →
Vì A , M , N , P đồng phẳng nên tồn tại các số x;y sao cho A P → = x A M → + y A N →
⇔ 1 2 A S → + A C → = x A S → + S M → + y A S → + S N →
⇔ 1 2 A S → + A S → + S B → + A S → + S D → = x A S → + S M → + y A S → + S N →
⇔ 3 2 A S → + 1 2 S B → + 1 2 S D → = x + y A S → + x m S M → + y n S N →
⇔ x + y = 3 2 x m = 1 2 y n = 1 2 ⇒ m + n = 3.
Ta có: V S . A N P V S . A B C = S N S B . S P S C ⇒ V S . A N P = S N S B . S P S C . V S . A B C = S N S B . 1 2 . V 2 1
V S . A M P V S . A D C = S M S D . S P S C ⇒ V S . A M P = S M S D . S P S C . V S . A D C = S M S D . 1 2 . V 2 2
Từ (1) và (2) V 1 V 2 = 1 4 S B S B + S M S D = 1 4 1 n + 1 m ≥ 1 m + n = 1 3
CM
12 tháng 1 2018
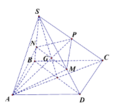
Gọi G là trọng tâm tam giác S A C ⇒ M N đi qua G
V 1 V = 1 2 V S A M N V S A B D + V S M N P V S B D C = 1 2 S M S D . S N S B + S P S C . S M S D . S N S B = 3 4 x . y
V 1 V = 1 2 V S A P N V S A C B + V S A M P V S A D C = 1 2 S P S C . S N S B + S M S D . S P S C = 1 4 x + y
Với x = S N S B ; Y = S M S D
⇒ 3 x y = x + y ≥ 2 x y ⇔ 9 x 2 y 2 ≥ 4 x y ⇔ 3 4 x y ≥ 1 3
Vậy V 1 V đạt giá trị nhỏ nhất bằng 1 3
Đáp án cần chọn là D