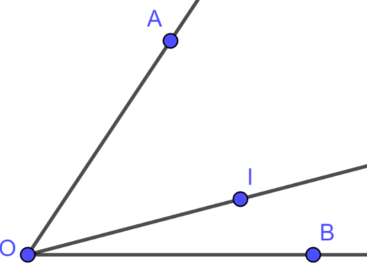
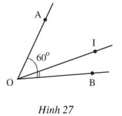
hình 27 cho biết OI nằm giữa hai tia OA,OB,góc AOB=60độ,góc BOI=1/4 góc AOB .Tính góc BOI,góc AOI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tui cx ms hok thôi
*Theo đề bài ,ta có \(\widehat{BOI}=\frac{1}{4}.\widehat{AOB}\)
Hay\(\widehat{BOI}=\frac{1}{4}.60\)
\(\Rightarrow\widehat{BOI}=15^0\)
*Vì tia OI nằm giữa hai tia OA,OB
Nên\(\widehat{AOI}+\widehat{IOB}=\widehat{AOB}\)
Hay\(\widehat{AOI}+15^o=60^0\)
\(\Rightarrow\widehat{AOI}=60^o-15^o=45^0\)
Vậy \(\widehat{AOI}=45^o\)

\(\widehat{BOI}=\frac{1}{4}\widehat{AOB}\Rightarrow\widehat{BOI}=\frac{1}{4}.60^o\Rightarrow\widehat{BOI}=15^o\)
Vì tia OI nằm giữa hai tia OA và OB
\(\Rightarrow\widehat{AOI}+\widehat{BOI}=\widehat{AOB}\)
Thay \(\widehat{BOI}=15^o,\widehat{AOB}=60^o\), ta có:
\(\widehat{AOI}+15^o=60^o\)
\(\Rightarrow\widehat{AOI}=60^o-15^o\)
\(\Rightarrow\widehat{AOI}=45^o\)
Vậy \(\widehat{BOI}=15^o,\widehat{AOI}=45^o\)


Ta có: \(\widehat{AOB}\)= 600 và \(\widehat{BOI}\)= \(\frac{1}{4}\)\(\widehat{AOB}\)
\(=>\widehat{BOI}\)= \(\frac{1}{4}.60\)
\(=>\widehat{BOI}\)= 150
Ta lại có: \(\widehat{BOI}\)\(+\widehat{AOI}\)= \(\widehat{AOB}\)
Hay: 150 + \(\widehat{AOI}\)= 600
=> \(\widehat{AOI}\)= 450
Vẽ hình hơi xấu, thông cảm nhé ^^
Hk tốt

TA CÓ: OI LÀ TIA NẰM GIỮA OA; OB
\(\Rightarrow\widehat{AOI}+\widehat{IOB}=\widehat{AOB}\)
MÀ: \(\widehat{AOI}=\frac{1}{4}\widehat{IOB}\)
THAY SỐ: \(\frac{1}{4}\widehat{IOB}+\widehat{IOB}=70^0\)
\(\Rightarrow\left(\frac{1}{4}+1\right)\widehat{IOB}=70^0\)
\(\frac{5}{4}\widehat{IOB}=70^0\)
\(\widehat{IOB}=70^0:\frac{5}{4}\)
\(\Rightarrow\widehat{IOB}=56^0\)
MÀ \(\widehat{AOI}=\frac{1}{4}\widehat{IOB}\)
THAY SỐ: \(\widehat{AOI}=\frac{1}{4}.56^0=14^0\)
\(\Rightarrow\widehat{AOI}=14^0\)
CHÚC BN HỌC TỐT!!!!!
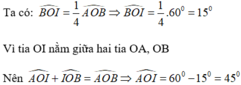

Ta có: \(\widehat{BOI}=\dfrac{1}{4}\cdot\widehat{AOB}\)(gt)
\(\Leftrightarrow\widehat{BOI}=\dfrac{1}{4}\cdot60^0\)
hay \(\widehat{BOI}=15^0\)
Ta có: tia OI nằm giữa hai tia OA và OB(gt)
nên \(\widehat{AOI}+\widehat{BOI}=\widehat{AOB}\)
\(\Leftrightarrow\widehat{AOI}=\widehat{AOB}-\widehat{BOI}=60^0-15^0\)
hay \(\widehat{AOI}=45^0\)
Vậy: \(\widehat{BOI}=15^0\); \(\widehat{AOI}=45^0\)