Nhờ ad duyệt ,ace giải giúp câu sau, xin cảm ơn ạ
Tìm số nguyên tố p, sao cho các số sau cũng là số nguyên tố:
1) p+2 và p + 10
2) p+2, p+6, p+8,p+12, p+14.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 12 2021
Gọi d là \(ƯCLN\left(3n+2,2n+1\right)\)
Ta có : 2n+ 1 chia hết cho d ,3n+2 chia hết cho d
\(3\left(2n+1\right)-2\left(3n+2\right)\)chia hết cho
1 chia hết cho d
\(d=1\)
Vậy \(3n+2;2n+1\)là số nguyên tố cùng nhau với mọi số tự nhiên n
25 tháng 12 2021
TL
Gọi d là ƯCLN(2n+1, 3n+2)
Ta có: 2n+1 chia hết cho d, 3n+2 chia hết cho d
=> 2(3n+2) - 3(2n+1) chia hết cho d
=> 1 chia hết cho d
=> d = 1
Vậy 2n+1 và 3n+2 là 2 số nguyên tố cùng nhau
HỌC TỐT Ạ
1
25 tháng 2 2021
Thử `p=2`
`=>p+2=4(HS)`
`=>p=2`(loại).
Thử `p=3`
`=>p+12=15(HS)`
`=>p=3`(loại).
Thử `p=5`
`=>` \begin{cases}p+2=7(SNT)\\p+6=11(SNT)\\p+8=13(SNT)\\p+12=17(SNT)\\p+14=19(SNT)\\\end{cases}
`=>p=5(TM)`
Nếu `p>5` mà p là SNT
`=>p cancel{vdost} 5`
`=>p=5k+1,5k+2,5k+3,5k+4`
`+)p=5k+1=>p+14=5k+15 vdots 5`
`=>p=5k+1` (loại).
`+)p=5k+2=>p+8=5k+10 vdots 5`
`=>p=5k+2` (loại).
`+)p=5k+3=>p+12=5k+15 vdots 5`
`=>p=5k+3` (loại).
`+)p=5k+4=>p+6=5k+10 vdots 5`
`=>p=5k+4` (loại).
Vậy `p=5`
1 tháng 11 2015
Bài 2 : c)
+Nếu p = 2 ⇒ p + 2 = 4 (loại)
+Nếu p = 3 ⇒ p + 6 = 9 (loại)
+Nếu p = 5 ⇒ p + 2 = 7, p + 6 = 11, p + 8 = 13, p + 12 = 17, p + 14 = 19 (thỏa mãn)
+Nếu p > 5, ta có vì p là số nguyên tố nên ⇒ p không chia hết cho 5 ⇒ p = 5k+1, p = 5k+2, p = 5k+3, p = 5k+4
-Với p = 5k + 1, ta có: p + 14 = 5k + 15 = 5 ( k+3) ⋮ 5 (loại)
-Với p = 5k + 2, ta có: p + 8 = 5k + 10 = 5 ( k+2 ) ⋮ 5 (loại)
-Với p = 5k + 3, ta có: p + 12 = 5k + 15 = 5 ( k+3) ⋮ 5 (loại)
-Với p = 5k + 4, ta có: p + 6 = 5k + 10 = 5 ( k+2) ⋮ 5 (loại)
⇒ không có giá trị nguyên tố p lớn hơn 5 thỏa mãn
Vậy p = 5 là giá trị cần tìm
Bài 4 : Tích của hai số tự nhiên là số nguyên tố nên một số là 1, số còn lại (kí hiệu a) là số nguyên tố.
Theo đề bài, 1 + a cũng là số nguyên tố. Xét hai trường hợp :
- Nếu 1 + a là số lẻ thì a là số chẵn. Do a là ....
Còn lại bạn tự làm nha , mình mỏi tay quá !
1 tháng 11 2015
a) +) p = 2 => p + 2 = 4 không là số nguyên tố => Loại
+) p = 3 => p+ 2 = 5; p + 10 = 13 là số nguyên tố (chọn)
+) p > 3:
Nếu p =3k + 1 thì p + 2 = 3k + 3 chia hết cho 3 => Loại
Nếu p = 3k + 2 thì p + 10 = 3k + 12 chia hết cho 3 => Loại
Vậy p = 3
b) tương tự câu a)
c)
+) p = 2 => p + 2 = 4 là hợp số => Loại
+) p = 3 => p + 6 = 9 là hợp số => Loại
+) p = 5 => p + 2 = 7; p+ 6 = 11; p + 8 = 13; p+ 12 = 17; p + 14 = 19 (Chọn)
+) p > 5:
Tương tự xét các trường hợp p = 5k + 1; 5k + 2; 5k + 3; 5k + 4 (loại)
Vậy p = 5
13 tháng 8 2021
Câu b:
Đến đoạn này cũng xét như câu a
Câu c:
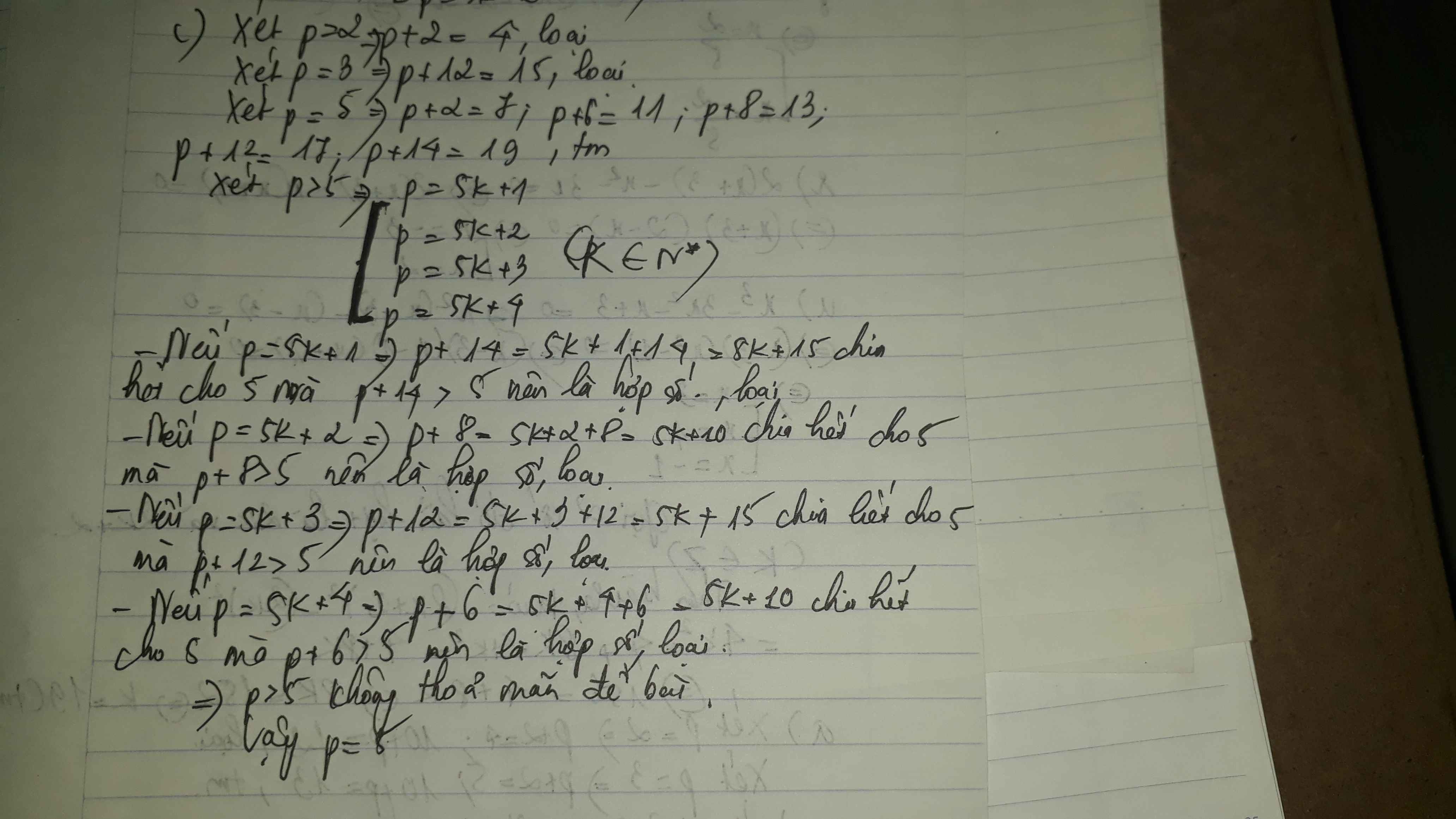
1, p = 3
2 ,p = 5
Nếu p = 2 = p + 2 = 4 ( loại )
Nếu p =3 = p + 6 = 9 ( loại )
Nếu p =5 = p + 2= 7 , p + 6 = 11 , p + 8 = 13 , p + 12 = 17 , p + 14 = 19 ( thỏa mãn )
Nếu p > 5 , ta có vì p là số nguyên tố nên p không chia hết cho 5 = p = 5k + 1 ,p = 5k + 2 , p = 5k + 3 , p = 5k+4
Với p = 5k + 1 ta có p +14 = 5k + 15 = 5 ( k + 3 ) không chia hết cho 5 ( loại )
Với p = 5k + 2 , ta có p + 8 = 5k + 10 ( k + 2 ) không chia hết cho 5 ( loại )
Với p= 5k + 3 , ta có p + 12 = 5k + 15 = 5 (k + 3 ) khồn chia hết 5 ( loaik )
Với p = 5k + 4 , ta có p + 6 = 5k + 10 = 5 ( k + 2 ) không chia hết cho 5 ( loại )
Không cos giá trị nào p = 5
p =5