Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


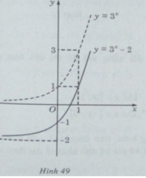
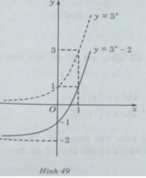
Đồ thị của hàm số y: y = 3 x − 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)

y = 2 – 3 x = −( 3 x − 2)
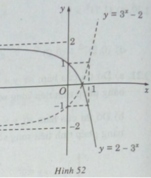
Ta có đồ thị của hàm số y = 2 − 3 x đối xứng với đồ thị cua hàm số y = 3 x – 2 qua trục hoành (H.52).

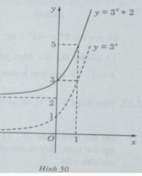
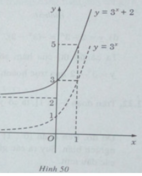
Đồ thị của hàm số y = 3 x + 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)

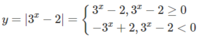
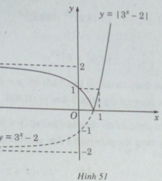
Do đó, đồ thị của hàm số y = | 3 x − 2| gồm:
- Phần đồ thị của hàm số y = 3 x − 2 ứng với 3 x – 2 ≥ 0 (nằm phía trên trục hoành).
- Phần đối xứng qua trục hoành của đồ thị hàm số y = 3 x − 2 ứng với 3 x – 2 < 0.
Vậy đồ thị của hàm số y = | 3 x − 2| có dạng như hình 51.

a: 
b: Để đồ thị hàm số y=(m+1)x-3 song song với đồ thị hàm số y=-3x+2 thì \(\left\{{}\begin{matrix}m+1=-3\\2\ne-3\left(đúng\right)\end{matrix}\right.\)
=>m+1=-3
=>m=-4

Đồ thị của hàm số Bài viết này không được chú giải bất kỳ nguồn tham khảo nào. ... Nếu đầu vào x là một cặp có thứ tự các số thực (x1, x2) thì đồ thị của hàm số f là tập hợp tất cả các bộ ba có thứ tự (x1, x2, f(x1, x2)), và đối với một hàm liên tục thì đó là một mặt.
Đồ thị của hàm số Bài viết này không được chú giải bất kỳ nguồn tham khảo nào. ... Nếu đầu vào x là một cặp có thứ tự các số thực (x1, x2) thì đồ thị của hàm số f là tập hợp tất cả các bộ ba có thứ tự (x1, x2, f(x1, x2)), và đối với một hàm liên tục thì đó là một mặt.
Cho hàm số y=-3x A) vẽ đồ thị hàm số B) biết đồ thị hàm số y=-3x đi qua điểm N(x0;9) tính giá trị x0

A)
cho x=1 => y=-3 => A(1;-3)
vậy đường thẳng OA là đồ thị hàm số y=-3x

a) Đồ thị của hàm số y: y = 3 x − 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)
b) Đồ thị của hàm số y = 3 x + 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)
c) 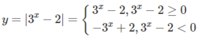
Do đó, đồ thị của hàm số y = | 3 x − 2| gồm:
- Phần đồ thị của hàm số y = 3 x − 2 ứng với 3 x – 2 ≥ 0 (nằm phía trên trục hoành).
- Phần đối xứng qua trục hoành của đồ thị hàm số y = 3 x − 2 ứng với 3 x – 2 < 0.
Vậy đồ thị của hàm số y = | 3 x − 2| có dạng như hình 51.
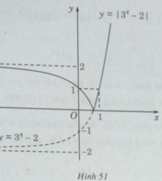
Ta có đồ thị của hàm số y = 2 − 3 x đối xứng với đồ thị cua hàm số y = 3 x – 2 qua trục hoành (H.52).
a) Vẽ đồ thị của hàm số: \(y = 0,5x;y = - 3x;y = x\).
b) Các đồ thị sau đây là đồ thị của hàm số nào?
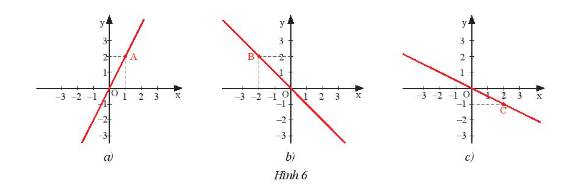

a)
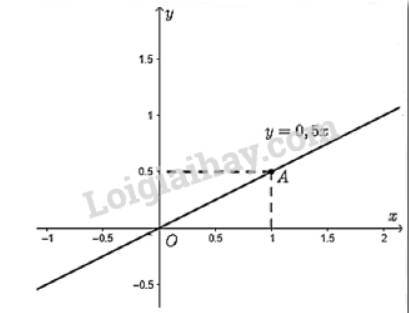
- Vẽ đồ thị hàm số \(y = 0,5x\)
Cho \(x = 1 \Rightarrow y = 0,5.1 = 0,5\). Ta vẽ điểm \(A\left( {1;0,5} \right)\)
Đồ thị hàm số \(y = 0,5x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;0,5} \right)\).
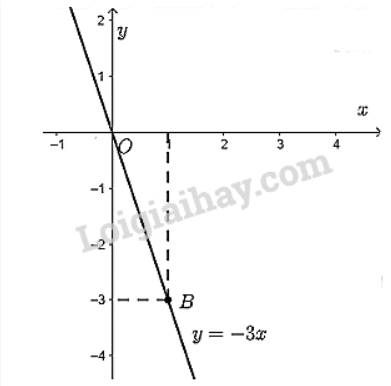
- Vẽ đồ thị hàm số \(y = - 3x\)
Cho \(x = 1 \Rightarrow y = - 3.1 = - 3\). Ta vẽ điểm \(B\left( {1; - 3} \right)\)
Đồ thị hàm số \(y = - 3x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(B\left( {1; - 3} \right)\).
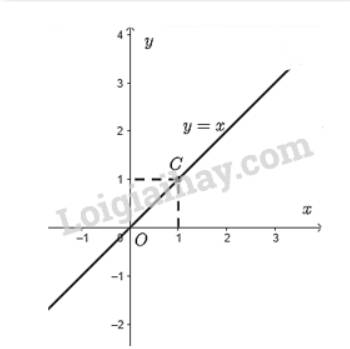
- Vẽ đồ thị hàm số \(y = x\)
Cho \(x = 1 \Rightarrow y = 1\). Ta vẽ điểm \(C\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(C\left( {1;1} \right)\).
b) Ta thấy cả ba đồ thị đều đi qua gốc tọa độ \(O\left( {0;0} \right)\) nên có dạng \(y = ax\).
- Ở đồ thị a, đồ thị hàm số đi qua điểm \(A\left( {1;2} \right)\) nên ta có: \(2 = a.1 \Rightarrow a = 2\).
Do đó, đồ thị a là đồ thị của hàm số \(y = 2x\).
- Ở đồ thị b, đồ thị hàm số đi qua điểm \(B\left( { - 2;2} \right)\) nên ta có: \(2 = a.\left( { - 2} \right) \Rightarrow a = 2:\left( { - 2} \right) = - 1\).
Do đó, đồ thị b là đồ thị của hàm số \(y = - x\).
- Ở đồ thị c, đồ thị hàm số đi qua điểm \(C\left( {2; - 1} \right)\) nên ta có: \( - 1 = a.2 \Rightarrow a = \left( { - 1} \right):2 = \dfrac{{ - 1}}{2}\).
Do đó, đồ thị b là đồ thị của hàm số \(y = \dfrac{{ - 1}}{2}x\).

Giải
a) y = f(x) = 3x
Cho x = 1 thì y = 3 .1 = 3 ; A(1;3)
b) y = f(x) = \(-\frac{1}{2}x\)
cho x = 2 thì y = 2 . \(-\frac{1}{2}\)= -1