Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(c,y=2x+2-2x=2\\ d,y=3x-3-x=2x-3\\ f,y=x+\dfrac{1}{x}=\dfrac{x^2+1}{x}\)
Hs bậc nhất là a,b,d,e
\(a,-2< 0\Rightarrow\text{nghịch biến}\\ b,\sqrt{2}>0\Rightarrow\text{đồng biến}\\ d,2>0\Rightarrow\text{đồng biến}\\ e,-\dfrac{2}{3}< 0\Rightarrow\text{nghịch biến}\)
b: Vì (d1)//(d) nên (d1): y=-2x+b
=>a=-2
Thay x=2 và y=1 vào (d1), ta được:
b-4=1
=>b=5
a: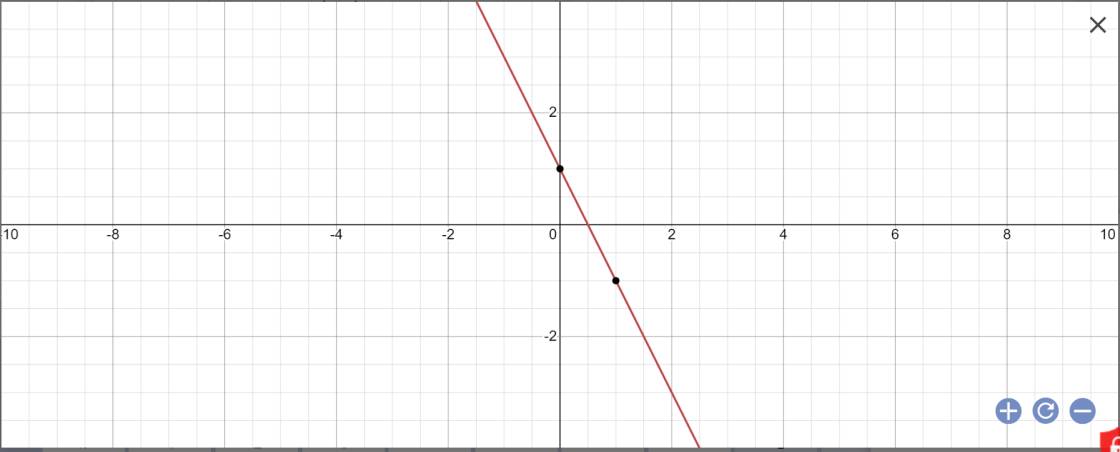 
Để d song song với d' thì \(\left\{{}\begin{matrix}m^2=2\\m\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\pm\sqrt{2}\\m\ne1\end{matrix}\right.\Leftrightarrow m\in\left\{\sqrt{2};-\sqrt{2}\right\}\)(1)
Để d' cắt trục hoành thì y=0
Thay y=0 vào hàm số \(y=m^2x+m\), ta được:
\(m^2x+m=0\)
\(\Leftrightarrow x\cdot m^2=-m\)
\(\Leftrightarrow x=\dfrac{-m}{m^2}=\dfrac{-1}{m}\)
Để d' cắt trục hoành tại điểm có hoành độ âm thì \(x< 0\)
\(\Leftrightarrow\dfrac{-1}{m}< 0\)
\(\Leftrightarrow m>0\)(2)
Từ (1) và (2) suy ra \(m=\sqrt{2}\)
Vậy: Để d//d' và d' cắt trục hoành tại điểm có hoành độ âm thì \(m=\sqrt{2}\)
b: Tọa độ giao điểm là:
2x-1=x+2 và y=x+2
=>3x=3 và y=x+2
=>x=1 và y=3
a: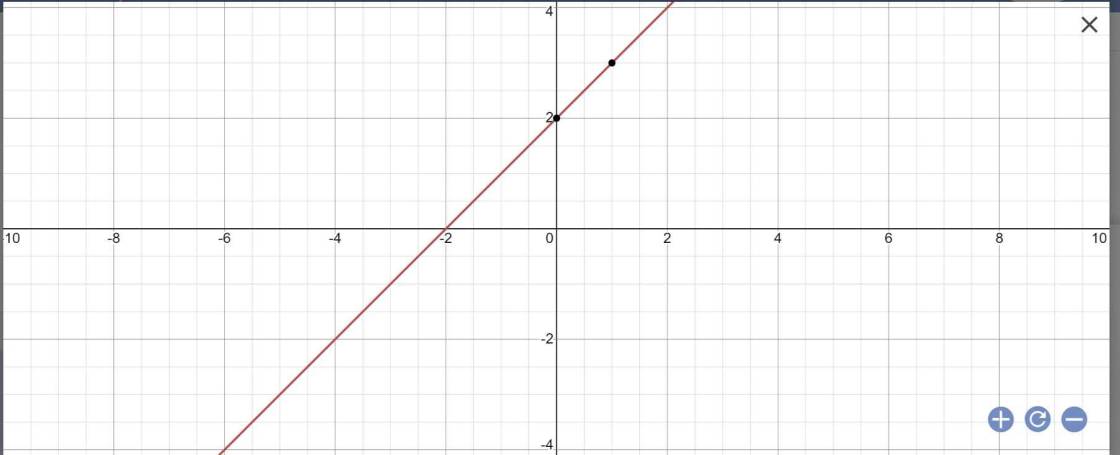 
a: Để hàm số nghịch biến trên R thì m-2<0
=>m<2
b: Thay x=-3 và y=0 vào (d), ta được:
-3(m-2)+m+3=0
=>-3m+6+m+3=0
=>-2m+9=0
=>-2m=-9
=>\(m=\dfrac{9}{2}\)
c: Tọa độ giao điểm của y=-x+2 và y=2x-1 là:
\(\left\{{}\begin{matrix}2x-1=-x+2\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=3\\y=-x+2\end{matrix}\right.\)
=>x=1 và y=-1+2=1
Thay x=1 và y=1 vào (d), ta được:
m+2+m+3=1
=>2m+5=1
=>2m=-4
=>m=-4/2=-2
a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)
b: Phương trình hoành độ giao điểm là:
2x+1=x+3
=>2x-x=3-1
=>x=2
Thay x=2 vào y=x+3, ta được:
y=2+3=5
a: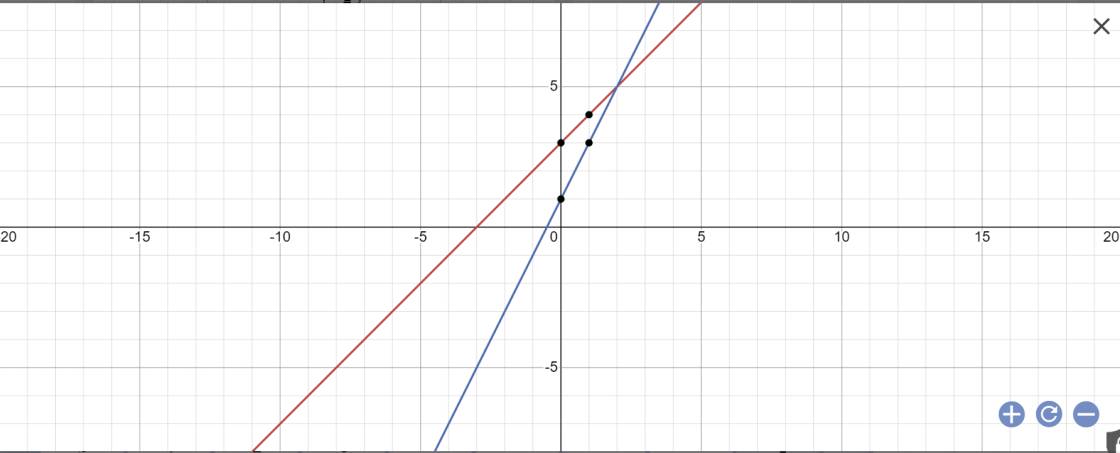 
Chọn A.
Phương trình hoành độ giao điểm:
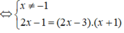
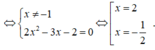
Vậy số giao điểm là 2.
