Cho hình thang cân ABCD đáy AB < CD. Gọi M, N lần lượt là trung điểm của AD và BC, MN giao BD tại I. Biết AD = 10cm, MI = 6cm, NI = 12cm. Tính diện tích tứ giác ABCD.
cần gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 1 2022
Do M, N là trung điểm của AD và BC nên Mn là đường trung bình của hình thang ABCD
⇒ MN // AB
Do vậy: MI // AB và NI // CD
Lại có: AB = 2MI = 12 ( cm ) ; CD = 2NI = 24 ( cm )
Kẻ AH ⊥ CD tại H và BK ⊥ CD tại K. Khi đó ABCD là hình thang cân nên:
AH = BK và DH = CK = \(\dfrac{DC-AB}{2}=\dfrac{24-12}{6}=6\left(cm\right)\)
Theo định lí Py - ta - go trong △ AHD ta có:
AH2 = AD2 - DH2 ⇒ AH = \(\sqrt{10^2-6^2}=8\left(cm\right)\)
Diện tích hình thang ABCD :
\(S_{ABCD}=\dfrac{\left(AB+CD\right).AH}{2}=\dfrac{\left(12+24\right).8}{2}=144\left(cm^2\right)\)
CM
1 tháng 4 2018
Xét hình thang ABCD có M và N lần lượt là trung điểm của AD và BC nên MN là đường trung bình của hình thang:
Suy ra: MN// AB// CD và
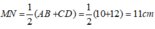
Suy ra: tứ giác MNCD là hình thang.
Vì M là trung điểm của AD và đường cao AH = 6cm nên chiều cao xuất phát từA của hình thang MNCD là:
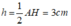
Diện tích hình thang ABNM là :
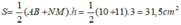
Chọn đáp án D
2 tháng 10 2021
a) Ta có: AB//CD(ABCD là hthang cân)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{OAB}=\widehat{ODC}\\\widehat{OBA}=\widehat{OCD}\end{matrix}\right.\)
Mà \(\widehat{ODC}=\widehat{OCD}\)(ABCD là hthang cân)
\(\Rightarrow\widehat{OBA}=\widehat{OAB}\)
=> Tam giác OAB cân tại O
b) Xét hthang ABCD có:
M là trung điểm AD(gt)
N là trung điểm BC(gt)
=> MN là đường trung bình
=> \(MN=\dfrac{AB+CD}{2}=\dfrac{6+10}{2}=8\left(cm\right)\)