Cho a/a'=b/b'=c/c'.tính giá trị biểu thức:(a-3b+2c)/(a'-3b'+2c')
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì \(a,b,c>0\Rightarrow a+b+c\ne0\)
Áp dụng tc dtsbn:
\(\dfrac{2b+c-a}{a}=\dfrac{2c-b+a}{b}=\dfrac{2a+b-c}{c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\\ \Rightarrow\left\{{}\begin{matrix}2b+c-a=2a\\2c-b+a=2b\\2a+b-c=2c\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3a-2b=c\\3b-2c=a\\3c-2a=b\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3a-c=2b\\3b-a=2c\\3c-b=2a\end{matrix}\right.\\ \Rightarrow P=\dfrac{abc}{2a\cdot2b\cdot2c}=\dfrac{1}{8}\)

\(\frac{a}{a^,}=\frac{b}{b^,}=\frac{c}{c^,}=-4\Rightarrow\)\(\frac{-a}{a^,}=\frac{-b}{b^,}=\frac{-c}{c^,}=\frac{-a+3b-2c}{a^,-3b^,+2c^,}=4\)
Vậy
\(\frac{-a+3b-2c}{a^,-3b^,+2c^,}=4\)

\(2a=3b=4c\\ \Leftrightarrow\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{2b}{8}=\dfrac{2c}{6}=\dfrac{a+b-c}{7}=\dfrac{a+2b-2c}{8}\\ \Leftrightarrow A=\dfrac{a+b-c}{a+2b-2c}=\dfrac{7}{8}\)

Ta có \(ab+bc+ca=3abc\)
\(\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\)
Đặt \(x=\dfrac{1}{a},y=\dfrac{1}{b},z=\dfrac{1}{c}\) thì ta có \(x,y,z>0;x+y+z=3\) và
\(\sqrt{\dfrac{a}{3b^2c^2+abc}}=\sqrt{\dfrac{\dfrac{1}{x}}{3.\dfrac{1}{y^2z^2}+\dfrac{1}{xyz}}}=\sqrt{\dfrac{\dfrac{1}{x}}{\dfrac{3x+yz}{xy^2z^2}}}=\sqrt{\dfrac{y^2z^2}{3x+yz}}\) \(=\dfrac{yz}{\sqrt{3x+yz}}\) \(=\dfrac{yz}{\sqrt{x\left(x+y+z\right)+yz}}\) \(=\dfrac{yz}{\sqrt{\left(x+y\right)\left(x+z\right)}}\)
Do đó \(T=\dfrac{yz}{\sqrt{\left(x+y\right)\left(x+z\right)}}+\dfrac{zx}{\sqrt{\left(y+z\right)\left(y+x\right)}}+\dfrac{xy}{\sqrt{\left(z+x\right)\left(z+y\right)}}\)
Lại có \(\dfrac{yz}{\sqrt{\left(x+y\right)\left(x+z\right)}}\le\dfrac{yz}{2\left(x+y\right)}+\dfrac{yz}{2\left(x+z\right)}\)
Lập 2 BĐT tương tự rồi cộng theo vế, ta được \(T\le\dfrac{yz}{2\left(x+y\right)}+\dfrac{yz}{2\left(x+z\right)}+\dfrac{zx}{2\left(y+z\right)}+\dfrac{zx}{2\left(y+x\right)}\) \(+\dfrac{xy}{2\left(z+x\right)}+\dfrac{xy}{2\left(z+y\right)}\)
\(T\le\dfrac{yz+zx}{2\left(x+y\right)}+\dfrac{xy+zx}{2\left(y+z\right)}+\dfrac{xy+yz}{2\left(z+x\right)}\)
\(T\le\dfrac{x+y+z}{2}\) (do \(x+y+z=3\))
\(T\le\dfrac{3}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=z=1\) \(\Leftrightarrow a=b=c=1\)
Vậy \(maxT=\dfrac{3}{2}\), xảy ra khi \(a=b=c=1\)
(Mình muốn gửi lời cảm ơn tới bạn Nguyễn Đức Trí vì ý tưởng của bài này chính là bài mình vừa hỏi lúc nãy trên diễn đàn. Cảm ơn bạn Trí rất nhiều vì đã giúp mình có được lời giải này.)
Bạn Lê Song Phương xem lại dùm nhé, thanks!
\(...\dfrac{yz}{\sqrt[]{\left(x+y\right)\left(x+z\right)}}\le\dfrac{2yz}{x+y}+\dfrac{2yz}{x+z}\)
\(...\Rightarrow T\le2.3=6\)
\(\Rightarrow GTLN\left(T\right)=6\left(tạia=b=c=1\right)\)

Sai đề! Sửa: that 2c+b-a=2c+a-b
Đặt 2a+b-c=x, 2b+c-a=y, 2c+a-b=z
\(\Rightarrow8\left(a+b+c\right)^3=\left(x+y+z\right)^3=x^3+y^3+z^3\)và \(P=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
Ta có: \(\left(x+y+z\right)^3-x^3-y^3-z^3=0\Leftrightarrow\left(x+y\right)^3+3\left(x+y\right)z\left(x+y+z\right)-x^3-y^3=0\)
\(\Leftrightarrow3xy\left(x+y\right)+3\left(x+y\right)z\left(x+y+z\right)=0\Leftrightarrow3\left(x+y\right)\left(xy+xz+yz+z^2\right)=0\)
\(\Leftrightarrow3\left(x+y\right)\left(y+z\right)\left(z+x\right)=0\Leftrightarrow3P=0\Leftrightarrow P=0\)

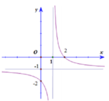
Đáp án A
Phương pháp: Dựa vào các đường tiệm cận và các điểm đi qua của đồ thị hàm số.
Cách giải:
Đồ thị hàm số y = a x + b x + c có đường TCĐ x = – c => – c = 1 <=> c = – 1, TCN y = a => a = –1
Đồ thị hàm số đi qua (0;–1)
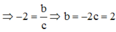
![]()
TFBOYS
Tứ diệp thảo
cỏ bốn lá
Vương Tuấn Khải :9/11/1999 (9x)
Vương Nguyên :8/11/2000(10x)
Dịch Dương Thiên Tỉ :28/11/2000(10x)
The Fighting Boys
Hẹn ước 10 năm
Karry biệt danh là : Nam thần karry ,Tiểu bàng giải , Cua nhỏ , anh đao .................
Roy biệt danh là: Tiểu thang viên , trôi nhi , nguyên nhi ,...........
Jackson biệt danh là : Thiên Chỉ Hạc , Thiên Thiên , Học bá , hạc nhỏ , cục bông , đùi gà ,.............
Mình là : fan KT