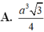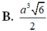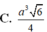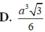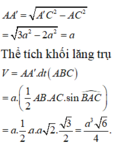Tam giác ABC có góc A=60o , AB = 5, AC = 8, Tính tích vecto AB→.BC→
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Y
3 tháng 3 2023
\(a,\overrightarrow{AB}=\left(2;10\right)\)
\(\overrightarrow{AC}=\left(-5;5\right)\)
\(\overrightarrow{BC}=\left(-7;-5\right)\)
\(b,\) Thiếu dữ kiện
\(c,Cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=\dfrac{\left|2\left(-5\right)+10.5\right|}{\sqrt{2^2+10^2}.\sqrt{\left(-5\right)^2+5^2}}=\dfrac{2\sqrt{13}}{13}\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{AC}\right)=56^o18'\)
\(Cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)=\dfrac{\left|2\left(-7\right)+10\left(-5\right)\right|}{\sqrt{2^2+10^2}.\sqrt{\left(-7\right)^2+\left(-5\right)^2}}\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{BC}\right)=43^o9'\)
CM
29 tháng 9 2017
Đáp án: C
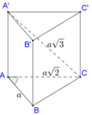
Gọi H là trung điểm BC ⇒ A ' H ⊥ ( A B C )
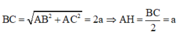
S ∆ A B C = 1 2 A B . A C = a 2 3 2
Kết luận V = a 3 . a 2 3 2 = 3 a 3 2
NT
1
MH
3 tháng 2 2021
Dựng \(AH\) vuông góc \(BC\). Đặt \(AB=x\Rightarrow AH=x.\sin60^0=\dfrac{x\sqrt{3}}{2};BH=x\cos60^0=\dfrac{x}{2}\)
\(\Rightarrow HC=BC-BH=8-\dfrac{x}{2};AC=12-x\)
Tam giác \(AHC\) vuông tại \(H\Rightarrow AC^2=AH^2+HC^2\Rightarrow\left(12-x\right)^2=\dfrac{3x^2}{4}+\left(8-\dfrac{x}{2}\right)^2\)
Giải phương trình trên ta được \(x=5\).
Vậy \(AB=5cm\).
6 tháng 1
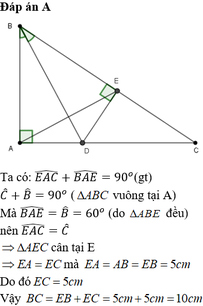
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>BA=BE
Xét ΔABE có BA=BE và \(\widehat{ABE}=60^0\)
nên ΔABE đều
c: Xét ΔABC vuông tại A có \(cosABC=\dfrac{AB}{BC}\)
=>\(\dfrac{5}{BC}=cos60=\dfrac{1}{2}\)
=>\(BC=5\cdot2=10\left(cm\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2021
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=-\dfrac{1}{32}\)
\(\Rightarrow A\approx92^0\)
\(p=\dfrac{AB+AC+BC}{2}=\dfrac{31}{2}\)
\(S_{ABC}=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}\simeq40\)
\(r=\dfrac{S}{p}=\dfrac{80}{31}\)