Cho hàm số $y = \dfrac{x+2}{2x+3}$ có đồ thị $(C)$. Đường thẳng $y=ax+b$ là tiếp tuyến của $(C)$ và cắt trục hoành tại $A$, cắt trục tung tại $B$ sao cho $AOB$ là tam giác vuông cân tại $O$, $O$ là gốc tọa độ. Xác định $a$ và $b$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
19 tháng 8 2018
Đáp án D
Phương pháp:
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x o .
+) Tìm giao điểm của tiếp tuyến với các trục tọa độ.
+) Tính OA, OB, giải phương trình tìm x o → Phương trình tiếp tuyến và kết luận.

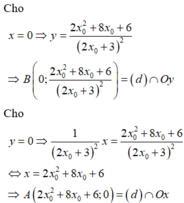
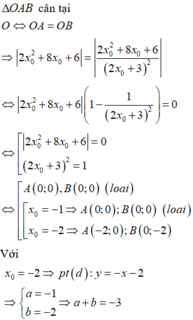

CM
25 tháng 5 2018
Chọn: D
![]()
![]()
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x 0 là:
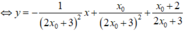
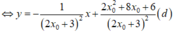
Cho x = 0
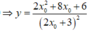
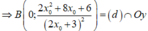
Cho y = 0
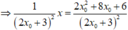
![]()
![]()
∆ O A B c â n t ạ i O ⇔ O A = O B
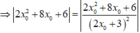
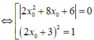
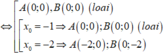
Với x 0 = - 2
![]()
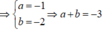
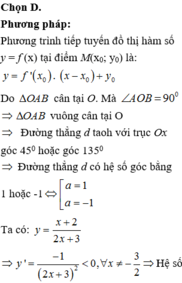
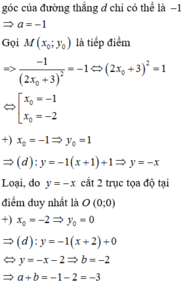






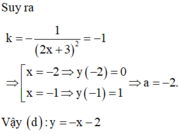
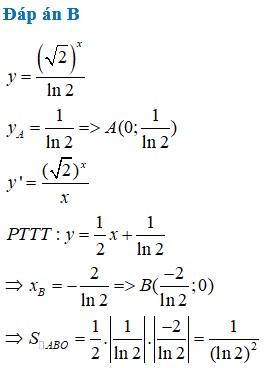


em gửi hình ảnh
y′=(2x+3)2−1.
Đường thẳng y = ax+by=ax+b là tiếp tuyến của đường cong (C)(C) khi hệ phương trình sau có nghiệm:
\left\{\begin{aligned} &\dfrac{x+2}{2x+3} = ax+b\\ &a = \dfrac{-1}{(2x+3)^2} (1)\\ \end{aligned}\right.⎩⎪⎪⎪⎨⎪⎪⎪⎧2x+3x+2=ax+ba=(2x+3)2−1(1)
Mà tiếp tuyến của (C)(C) cắt trục hoành tại AA, cắt trục tung tại BB sao cho AOBAOB là tam giác vuông cân tại OO nên a = -1a=−1 và b \ne 0 (2).b=0(2).
Từ (1)(1) và (2)(2) suy ra \left[\begin{aligned} &2x+3=1\\ &2x+3=-1\\ \end{aligned}\right. \Leftrightarrow \left[\begin{aligned} &x = -1\\ &x = -2\\ \end{aligned}\right. \Leftrightarrow \left[\begin{aligned} &b = 0 (l)\\ &b = -2 (tm) \end{aligned}\right. \Rightarrow a+b = -3.[2x+3=12x+3=−1⇔[x=−1x=−2⇔[b=0(l)b=−2(tm)⇒a+b=−3.