Cho hàm số $y = -\dfrac13x^3-2x^2-3x+1$ có đồ thị $(C)$. Trong các tiếp tuyến với $(C)$, tiếp tuyến có hệ số góc lớn nhất bằng bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 2 2022
Ta có y’ = -3x2 – 6x + 9
Gọi xo là hoành độ tiếp điểm của tiếp tuyến, ta có f’(xo) = -3xo2 – 6xo + 9
⇔ f’(xo) = -3(xo2 + 2xo + 1) + 12 = -3(xo + 1)2 + 12 ≤ 12
Từ đó suy ra maxf’(xo) = 12 tại xo = -1.
Với xo = -1 ⇒ yo = -16, phương trình tiếp tuyến cần tìm: y = 12x - 4.
Chúc bn học tốt
CM
21 tháng 8 2018
Đáp án B
Có
y ' = x 2 − 2 x + 2 y ' ' = 6 x − 2
Tiếp tuyến có hệ số góc nhỏ nhất là nghiệm của y ' ' = 0 ⇔ x = 1 3
⇒ y ' 1 3 = 5 3
, y’ đạt giá trị nhỏ nhất bằng –5 tại x = –1.
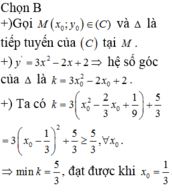
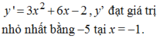
Xét tiếp tuyênd với (C) tại điểm có hoành độ x0 bất kì trên (C)
Khi đó hệ số góc của tiếp tuyến đó là: y'=-x20-4x0-3=1-(x0+2) =< 1 với mọi x
k=1