Hình thang ABCD có 2 đáy AB, CD với AB = 5. CD. P/g góc ABC cắt AD ở E và EA = 3ED. BE chia hình thang thành 2 tứ giác. Tính tỉ số diện tích 2 tam giác đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có S 1= S QAM =1/2 S QAB(2 tam giác cùng chiều cao hạ từ đỉnh Q và đáy AM = 1/2 AB)
và S BQA =1/2 S BDA (2 tam giác cùng chiều cao hạ từ đỉnh B và đáy AQ = 1/2 AD)
=>S 1=1/4 S ABD
*Tương tự:
S 2 = 1/4 S ABC
S 3 = 1/4 S BCD
S 4 = 1/4 S ACD
=> S 1+ S 2+ S 3+ S 4 = 1/4 S (ABD + ABC + BCD + ACD) = 1/4 S (ABCD x 2) = 1/2 S ABCD
=> S MNPQ = S ABCD - 1/2 S ABCD = 1/2 S ABCD
Kết luận: S MNPQ=1/2 S ABCD

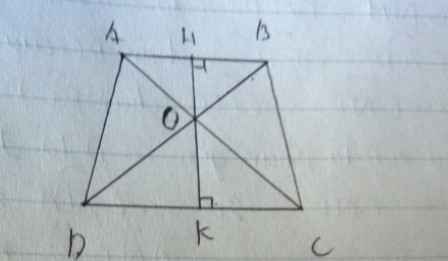
\(ABssCD\Rightarrow\dfrac{AB}{CD}=\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
a)\(S_{AOD}=\dfrac{1}{2}OA.OD.sinAOB\)
\(S_{BOC}=\dfrac{1}{2}OB.OC.sinBOC\)
\(\Rightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{OA.OD}{OB.OC}\) vì \(\widehat{AOD}=\widehat{BOC}\Rightarrow sinAOD=sinBOC\)
\(\Leftrightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{2}{3}.\dfrac{3}{2}=1\)
b) vì \(ABssCD\Rightarrow\dfrac{OH}{OK}=\dfrac{2}{3}\Rightarrow\dfrac{OH}{HK}=\dfrac{2}{5}\)
\(S_{AOB}=\dfrac{1}{2}.OH.AB\\ S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{1}{2}\left(AB+\dfrac{3}{2}AB\right).HK=\dfrac{1}{2}.\dfrac{5}{2}AB.HK\)
\(\Rightarrow\dfrac{S_{AOB}}{S_{ABCD}}=\dfrac{\dfrac{1}{2}OH.AB}{\dfrac{1}{2}HK.\dfrac{5}{2}AB}=\dfrac{2}{5}.\dfrac{1}{\dfrac{5}{2}}=\dfrac{4}{25}\)
\(\Rightarrow S_{ABCD}=\dfrac{4}{\dfrac{4}{25}}=25\)

Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E

Ủa sao lại 2 tam giác hay 2 tứ giác nhỉ? BE chia hình thang thành 1 tam giác và 1 tứ giác chứ?
Hướng dẫn là em kéo dài AD và BC cắt nhau tại F. Sử dụng định lý Talet
\(\dfrac{DF}{AF}=\dfrac{CD}{AB}=\dfrac{1}{5}\) \(\Rightarrow\dfrac{DF}{AD}=\dfrac{1}{4}\) ; \(\dfrac{AD}{AF}=\dfrac{4}{5}\)
\(EA=3DE\Rightarrow\dfrac{AE}{AD}=\dfrac{3}{4}\Rightarrow\dfrac{AE}{AF}=\dfrac{3}{5}\)
Từ E, D, F hạ vuông góc xuống AB tại G, H, I, FI cắt CD tại J
Talet: \(FJ=\dfrac{1}{5}FI\) ; \(\dfrac{DH}{FI}=\dfrac{AD}{AF}=\dfrac{4}{5}\Rightarrow DH=\dfrac{4}{5}FI\) ; \(\dfrac{EG}{FI}=\dfrac{AE}{AF}=\dfrac{3}{5}\Rightarrow EG=\dfrac{3}{5}FI\)
\(S_{ABF}=\dfrac{1}{2}FI.AB\)
\(S_{DCF}=\dfrac{1}{2}FJ.DC=\dfrac{1}{2}.\dfrac{1}{5}FI.\dfrac{1}{5}AB=\dfrac{1}{25}\left(\dfrac{1}{2}FI.AB\right)=\dfrac{1}{25}S_{ABF}\)
\(\Rightarrow S_{ABCD}=S_{ABF}-S_{CDF}=\dfrac{24}{25}S_{ABF}\)
\(S_{ABE}=\dfrac{1}{2}EG.AB=\dfrac{1}{2}.\dfrac{3}{5}FI.AB=\dfrac{3}{5}S_{ABF}\)
\(\Rightarrow S_{BCDE}=S_{ABCD}-S_{ABE}=\dfrac{24}{25}S_{ABF}-\dfrac{3}{5}S_{ABF}=\dfrac{9}{25}S_{ABF}\)
\(\Rightarrow\dfrac{S_{ABE}}{S_{BCDE}}=\dfrac{\dfrac{3}{5}S_{ABF}}{\dfrac{9}{25}S_{ABF}}=\dfrac{5}{3}\)
Chi tiết phân giác góc B thừa, ko cần sử dụng