tìm giá trị biểu thức \(J=C_{20}^0-2^2C^1_{20}+2^4C^2_{20}-...+2^{40}C^{20}_{20}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C
2
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 2 2023
Xét khai triển:
\(\left(x+1\right)^{20}=C_{20}^0+C_{20}^1x+C_{20}^2x^2+...+C_{20}^{20}x^{20}\)
Chia 2 vế cho x ta được:
\(\dfrac{\left(x+1\right)^{20}}{x}=\dfrac{1}{x}+C_{20}^1+C_{20}^2x+...+C_{20}^{20}.x^{19}\)
Thay \(x=2\)
\(\Rightarrow\dfrac{3^{20}}{2}=\dfrac{1}{2}+C_{20}^1+2C_{20}^2+2^2C_{20}^3+...+2^{19}C_{20}^{20}\)
\(\Rightarrow S=\dfrac{3^{20}-1}{2}\)
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Để tính \(A_{15}^{10}\) ta ấn liên tiếp các phím
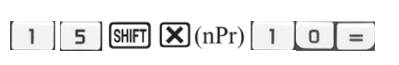
Thì nhận được kết quả là \(1,{08972864.10^{10}}\)
b) Để tính \(C_{10}^6 + C_{10}^7 + C_{11}^8\) thì ta ấn liên tiếp các phím
Thì ta nhận được kết quả là 495
c) Để tính \(C_5^1C_{20}^2 + C_5^2C_{20}^1\) thì ta ấn liên tiếp các phím
Thì ta được kết quả là 1150
AH
Akai Haruma
Giáo viên
28 tháng 7
1.
Ta thấy $(x-13)^2\geq 0$ với mọi $x$
$\Rightarrow T=(x-13)^2-26\geq 0-26=-26$
Vậy GTNN của $T$ là $-26$.
Giá trị này đạt tại $x-13=0\Leftrightarrow x=13$
AH
Akai Haruma
Giáo viên
28 tháng 7
2.
Ta thấy: $(x-14)^2\geq 0$ với mọi $x$
$\Rightarrow M=20-(x-14)^2\leq 20-0=20$
Vậy $M_{\max}=20$. Giá trị này đạt tại $x-14=0$
Hay $x=14$.
11 tháng 4 2022
-Có \(\left|x+1\right|+\left(y-2\right)^2=0\)
-Vì \(\left|x+1\right|\ge0\forall x;\left(y-2\right)^2\ge0\forall y\)
\(\Rightarrow\left|x+1\right|=0\) ; \(\left(y-2\right)^2=0\)
\(\Rightarrow x=-1;y=2\)
-Thay \(x=-1;y=2\) vào \(C=2x^6y-3xy^3-20\) ta được:
\(C=2.\left(-1\right)^6.2-3.\left(-1\right).2^3-20=8\)
26 tháng 12 2021
\(C=x^2-8x+20\\ C=x^2-8x+16+4\\ C=\left(x-4\right)^2+4\ge4\)
\(MinC=0\Leftrightarrow x-4=0\Leftrightarrow x=4\\ MinC=4\Leftrightarrow x=4\)
26 tháng 11 2016
Ta có : R = \(9x^2\) - \(6xy+2y^2\) + \(5\)
= \(\left(3x\right)^2\) - \(2.3x.\sqrt{2}^2\) + \(\left(\sqrt{2}y\right)^2\) + 5
= \(\left(3x-\sqrt{2}y\right)^2\) + 5
Vậy min R = 5 khi \(\left(3x-\sqrt{2}y\right)^2\) =0
28 tháng 1 2022
Sao em viết chữ giống anh mà bố mẹ em bảo xấu mà người khác mà viết thế bố mẹ em bảo đẹp thế là thế nào nhỉ?
Xét khai triển:
\(\left(x^2-1\right)^{20}=C_{20}^0-C_{20}^1.x^2+C_{20}^2x^4-...+C_{20}^{20}x^{20}\)
Thay \(x=2\)
\(\Rightarrow3^{20}=C_{20}^0-2^2C_{20}^1+2^4C_{20}^2-...+2^{40}C_{20}^{20}\)
\(\Rightarrow J=3^{20}\)