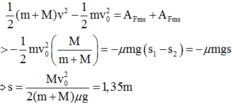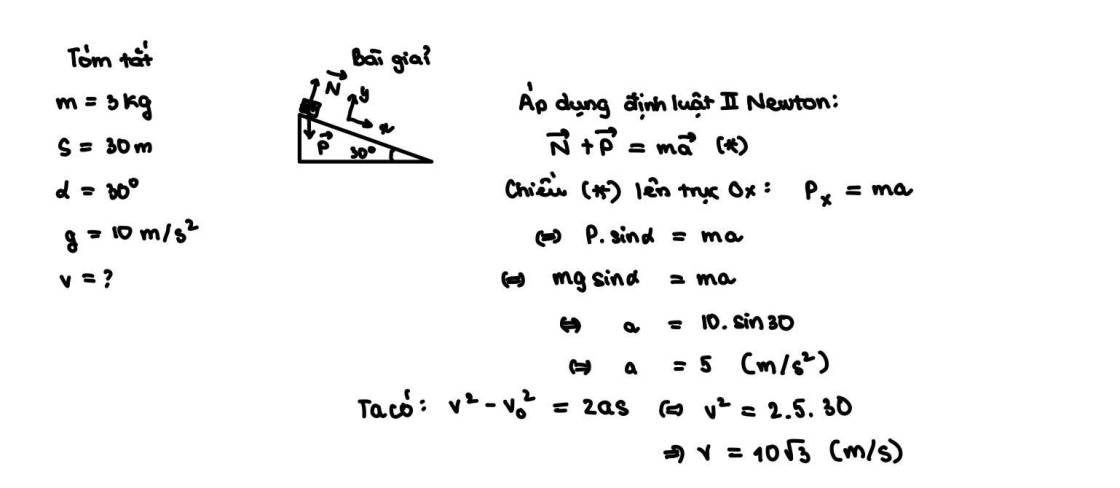.Một em bé trượt không vận tốc đầu từ đỉnh ván trượt nghiêng góc α đối với phương ngang. Lấy g=9,8(m/s bình). Lực nén của em bé lên ván trượt là 98 (N), khối lượng của em bé là 20(kg). Bỏ qua ma sát. Tìm góc α.
Giúp em với mn, giúp em vẽ hình với mn ới, em cám ơn nhìu lắm ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để tính tốc độ của vật trượt, ta sử dụng công thức:
v = sqrt(2 * g * h)
trong đó:
v là tốc độ của vật (m/s)g là lực trọng (m/s²)h là độ cao của vật từ đỉnh dốc xuống (m)Áp dụng công thức trên vào bài toán:
v = sqrt(2 * 10 * 30) = sqrt(6000) = 75 m/s
Kết quả:
Tốc độ của vật trượt (m/s) = 75 m/sTừ đây, ta có thể nhận thấy tốc độ của vật nặng 3 kg trượt không vận tốc ban đầu từ đỉnh một phẳng nghiêng dài 30 m mặt phẳng nghiêng một góc 30 độ so với phương ngang bỏ qua mọi ma sát và lực cản lấy g=10 m/s² là 75 m/s.

a. Từ thế năng trọng trường sang động năng và công của lực ma sát
- Năng lượng có ích: chuyển hoá thành động năng
- Năng lượng hao phí: chuyển hoá thành công lực ma sát
b. Ta có: \(\left\{{}\begin{matrix}W_1=mghsin\alpha=20\cdot10\cdot4\cdot sin30^0=400J\\W_2=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot20\cdot4^2=160J\end{matrix}\right.\)
\(\Rightarrow H=\dfrac{W_2}{W_1}100\%=\dfrac{160}{400}100\%=40\%\)

\(\left\{{}\begin{matrix}Ox:mg\sin\alpha-F_{ms}=m.a\\Oy:N=mg\cos\alpha\end{matrix}\right.\Rightarrow mg\sin\alpha-\mu mg\cos\alpha=ma\)
\(\Rightarrow a=g\sin\alpha-\mu g\cos\alpha=...\left(m/s^2\right)\)

Hình 21.3Ga
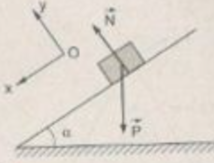
Phương trình chuyển động của vật trên các trục Ox, Oy là
Ox: Psina = ma (1)
Oy : N - Pcosa = 0 (2)
Mặt khác, theo bài ra : a = 2s/ t 2 (3)
Từ (1), (2) và (3) suy ra sin α = a/g = 2s/(g t 2 ) = 2.2,45/(9,8.1) = 0,5
⇒ α = 30 °

200g=0,2kg
các lực tác dụng lên vật khi ở trên mặt phẳng nghiêng
\(\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
chiếu lên trục Ox có phương song song với mặt phẳng nghiêng, chiều dương cùng chiều chuyển động
P.sin\(\alpha\)=m.a\(\Rightarrow\)a=5m/s2
vận tốc vật khi xuống tới chân dốc
v2-v02=2as\(\Rightarrow\)v=\(4\sqrt{5}\)m/s
khi xuống chân dốc trượt trên mặt phẳng ngang xuất hiện ma sát
các lực tác dụng lên vật lúc này
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a'}\)
chiếu lên trục Ox có phương nằm ngang chiều dương cùng chiều chuyển động của vật
-Fms=m.a'\(\Rightarrow-\mu.N=m.a'\) (1)
chiếu lên trục Oy có phương thẳng đứng chiều dương hướng lên trên
N=P=m.g (2)
từ (1),(2)\(\Rightarrow\)a'=-2m/s2
thời gian vật chuyển động trên mặt phẳng đến khi dừng lại là (v1=0)
t=\(\dfrac{v_1-v}{a'}\)=\(2\sqrt{5}s\)

Đáp án A
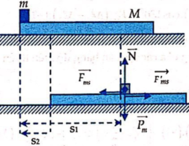
+ Ngoại lực tác dụng lên hệ 2 vật chỉ có phương thẳng đứng => Động lượng hệ bảo toàn theo phương ngang.
+ Khi m dừng lại trên M thì 2 vật chuyển động với cùng vận tốc v.
+ Áp dụng ĐLBTĐL cho thời điểm ban đầu và khi m dừng lại trên M:
![]()
+ Theo phương ngang m và M chịu của![]()
+ s1, s2 là quãng đường m và M chuyển động được tới khi m dừng lại trên M, quãng đường m trượt được trên M là s=s1- s2
+ Áp dụng định lý động năng: