Gọi x 1 ; x 2 l à n g h i ệ m c ủ a p h ư ơ n g t r ì n h \(x^2-3x-7\) .Tính: \(2x_1^3-3x_1^{2^{ }}x_2+2x_2^3-3x_1x_2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


-1/7 . 7/3 ; -4 ; -43/10
=-7/3 ; -4 ; -43/10
nhớ tính lại từ đây nha=-7/3 ; -4/1 ; -43/10
= -7/3 . -1/4 ; -43 /10
= 8/12; -43/10
=8/12 . -10/43
= -80/516

Lời giải:
Vì $x,y$ là 2 đại lượng tỉ lệ nghịch nên tích $xy=k$ không đổi với $k$ là số thực, hay còn được gọi là hệ số tỉ lệ.
Có:
$x_1y_1=x_2y_2=k$
$\Rightarrow 6y_1=-9y_2$
$\Rightarrow \frac{y_1}{-9}=\frac{y_2}{6}$
Áp dụng TCDTSBN: $\frac{y_1}{-9}=\frac{y_2}{6}=\frac{y_1-y_2}{-9-6}=\frac{10}{-15}=\frac{-2}{3}$
$\Rightarrow y_1=\frac{-2}{3}.(-9)=6; y_2=\frac{-2}{3}.6=-4$

Chọn C
Điều kiện
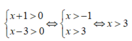
Ta có: log5(x+1) + log5( x-3) = 1
Tương đương : log5[(x+1)( x-3)] = 1 hay ( x+1) (x-3) = 5
=> x2- 3x+ x- 3= 5 nên x2- 2x-8= 0
Do đó; x= -2 hoặc x= 4
Mà x= -2 loại do đó đáp án đúng là C .

Bài 1
1)
a) x²(x - 2y) - 3xy(x - 2y)
= x(x - 2y)(x - 3y)
b) x² + 2xy + y² - 9z²
= (x² + 2xy + y²) - 9z²
= (x + y)² - (3z)²
= (x + y + 3z)(x + y - 3z)
2) 5x(x - 3) - x + 3 = 0
5x(x - 3) - (x - 3) = 0
(x - 3)(5x - 1) = 0
x - 3 = 0 hoặc 5x - 1 = 0
*) x - 3 = 0
x = 0 + 3
x = 3
*) 5x - 1 = 0
5x = 1
x = 1/5
Vậy x = 1/5; x = 3

a)
+) Ta có: a=3128 suy ra \(x = 3130\).
\(\left| {a - x} \right| = \left| {3128 - 3130} \right| = \left| { - 2} \right| = 2 \le 5\)
Vậy \(\left| {a - x} \right| \le 5\).
+) Ta có:
\(\begin{array}{l}x - 5 = 3128 - 5 = 3123\\x + 5 = 3128 + 5 = 3133\end{array}\)
Nên \(x - 5 \le a \le x + 5\)
b) Do y là số làm tròn đến hàng phần trăm của \(\frac{1}{3}\) nên \(y = 0,33\).
Ta có: \(\left| {\frac{1}{3} - y} \right| = \left| {\frac{1}{3} - 0,33} \right| = \left| {\frac{1}{{300}}} \right| = \frac{1}{{300}} = 0,00\left( 3 \right) \le 0,005\).
Nên \(\left| {\frac{1}{3} - y} \right| \le 0,005\).
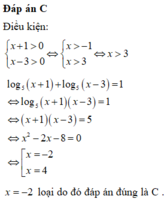
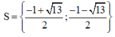
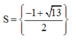


Ta có \(a=1;b=-3;c=-7\)
Nhận thấy a và c trái dấu, do đó phương trình đã cho luôn có hai nghiệm phân biệt \(x_1;x_2\)
Theo định lý Vi-ét, ta có: \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=-\frac{-3}{1}=3\\x_1x_2=\frac{c}{a}=\frac{-7}{1}=-7\end{cases}}\)
Như vậy đặt \(A=2x_1^3-3x_1^2x_2+2x_2^3-3x_1x_2\)\(=2\left(x_1^3+x_2^3\right)-3x_1x_2\left(x_1-1\right)\)
\(=2\left(x_1+x_2\right)\left(x_1^2-x_1x_2+x_2^2\right)-3.\left(-7\right)\left(x_1-1\right)\)(vì \(x_1x_2=-7\left(cmt\right)\))
\(=2.3\left(x_1^2+2x_1x_2+x_2^2-3x_1x_2\right)+21\left(x_1-1\right)\)(vì \(x_1+x_2=3\left(cmt\right)\))
\(=6\left[\left(x_1+x_2\right)^2-3.\left(-7\right)\right]+21x_1-21\)
\(=6\left(3^2+21\right)+21x_1-1\)\(=6.30+21x_1-1\)\(=179+21x_1\)
Xét phương trình \(x^2-3x-7=0\)có hai nghiệm phân biệt \(x_1,x_2\), do đó có hai trường hợp của \(x_1\)
\(\orbr{\begin{cases}x_1=\frac{-b+\sqrt{b^2-4ac}}{2a}=\frac{-\left(-3\right)+\sqrt{\left(-3\right)^2-4.1.\left(-7\right)}}{2.1}=\frac{3+\sqrt{9+28}}{2}=\frac{3+\sqrt{37}}{2}\\x_2=\frac{-b-\sqrt{b^2-4ac}}{2a}=\frac{-\left(-3\right)-\sqrt{\left(-3\right)^2-4.1.\left(-7\right)}}{2.1}=\frac{3-\sqrt{9+28}}{2}=\frac{3-\sqrt{37}}{2}\end{cases}}\)
Trường hợp \(x_1=\frac{3+\sqrt{37}}{2}\)thì \(A=179+21x_1=179+21.\frac{3+\sqrt{37}}{2}=\frac{358+63+21\sqrt{37}}{2}=\frac{421+21\sqrt{37}}{2}\)
Trường hợp \(x_1=\frac{3-\sqrt{37}}{2}\)thì
\(A=179+21x_1=179+21.\frac{3-\sqrt{37}}{2}=\frac{358+63-21\sqrt{37}}{2}=\frac{421-21\sqrt{37}}{2}\)
Vậy ...