cho tam giác ABC vuông tại A .Đường cao AH.Trên cạnh BC lấy điểm E sao cho BE=BA.Vẽ EK vuông góc với AC(K THUỘC AC). CMR AK=AH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
FF
16 tháng 7 2016
Nối A và E lại ta có tam giác BAE cân tại B (vì BE=BA). Ta có góc BAE + góc CAE = góc ABC
=90 độ. Mặt khác góc CAE + góc AEK = góc EKA = 90 độ => góc BAE = góc AEK. Mà góc BAE = góc BEA (tam giác BAE cân tại B) => góc AEK = góc BEA. Xét tam giác vuông AHE và AKE bằng nhau theo trường hợp cạnh góc vuông (AE chung) góc nhọn kề (góc AEK = góc BEA) => AK = AH (đpcm)
11 tháng 5 2022
a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của góc HAC
YP
11 tháng 5 2022
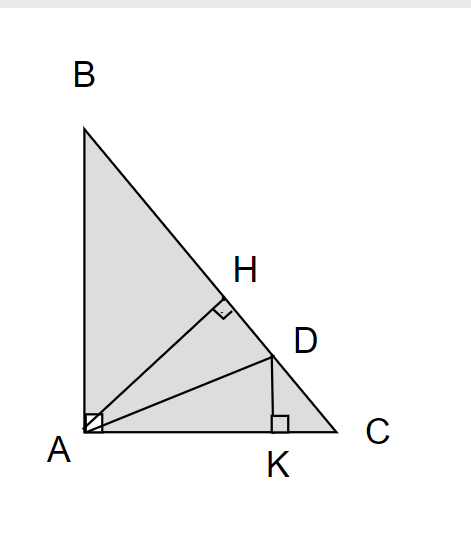
c, Ta có: Góc CAD= góc HAD
hay góc KAD= góc HAD
Xét △ AHD và △AKD có:
AD chung
Góc AHD= góc AKD= 90 độ
Góc KAD= góc HAD
=> △AHD= △AKD (cạnh huyền- góc nhọn)
=> AH= AK (2 cạnh tương ứng)
17 tháng 2 2017
∆AKE vuông tại K => ∠AEK + ∠EAK = 900 => ∠EAK = 900 - ∠EAK (1)
∠BAE + ∠EAK = 900 => ∠BAE = 900 - ∠EAK (2)
Từ (1) ; (2) => ∠AEK = ∠BAE (3)
Vì AB = BE (gt) => ∆ ABE cân tại B => ∠BAE = ∠BEA (theo định lý) (4)
Từ (3) ; (4) => ∠AEK = ∠BEA (5)
Xét ∆AHE và ∆AKE có :
∠AHE = ∠AKE = 900 (gt)
Cạnh AE chung
∠AEK = ∠BEA ( theo (5) )
=> ∆AHE = ∆AKE (CH - GN)
=> AK = AH (cạnh T/Ư)
Vậy AK = AH
18 tháng 3 2020
kẻ EM _|_ AB
xét tam giác EMB và tam giác AHB có : ^B chung
^EMB = ^AHB = 90
BE = BA (gt)
=> tam giác EMB = tam giác AHB(ch-gn)
=> AH = EM (đn) (1)
EK _|_ AC (gt)
AB _|_ AC (gt)
=> EK // AB (đl)
=> ^KEA = ^EAM (slt)
xét tam giác AEK và tam giác EAM có : AE chung
^EKA = ^AME = 90
=> tam giác AEK = tam giác EAM (ch-gn) (2)
=> AK = EM và (1)
=> AK = AH
tam giác EMB = tam giác AHB (cmt) => BM = BH (Đn)
BE = BA (Gt)
BH + HE = BE
BM + MA = BA
=> HE = MA
gọi EM cắt AH tại O; xét tam giác EOH và tam giác AOM có : ^EHO = ^AMO = 90
^OEH = ^OAM do tam giác EMB = tam giác AHB (cmt)
=> tam giác OEH = tam giác AOM (cgv-gnk)
=> EH = AM (Đn)
(2) => KE = AM
=> KE = EH