Giúp em với mai nộp rồi 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DP
31 tháng 10 2021
xét tứ giác ANMP có
góc NAP = 90 độ ( AB vuông góc AC)
góc MPA = 90 độ (MP vuông góc AC)
Góc ANM = 90 độ (MN vuông góc AB)
=> tứ giác AMNP là hình chữ nhật
17 tháng 9 2021
a: Ta có: \(a^3+b^3+c^3-3abc\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)\)
9 tháng 11 2023
Gọi tia đối của tia AB là AE
=>AD là phân giác của \(\widehat{EAC}\)
Xét ΔABC có \(\widehat{EAC}\) là góc ngoài tại đỉnh A
nên \(\widehat{EAC}=\widehat{ABC}+\widehat{ACB}=80^0\)
AD là phân giác của góc EAC
=>\(\widehat{EAD}=\widehat{CAD}=\dfrac{\widehat{EAC}}{2}=\dfrac{80^0}{2}=40^0\)
\(\widehat{DAC}=\widehat{ACB}\left(=40^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
HP
12 tháng 9 2021
b, \(cos^25x-sin^2x=0\)
\(\Leftrightarrow cos^25x-cos^2\left(x-\dfrac{\pi}{2}\right)=0\)
\(\Leftrightarrow\left[cos5x-cos\left(x-\dfrac{\pi}{2}\right)\right]\left[cos5x+cos\left(x-\dfrac{\pi}{2}\right)\right]=0\)
\(\Leftrightarrow-4sin\left(3x-\dfrac{\pi}{4}\right).sin\left(2x+\dfrac{\pi}{4}\right).cos\left(3x-\dfrac{\pi}{4}\right).cos\left(2x+\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow-sin\left(6x-\dfrac{\pi}{2}\right).sin\left(4x+\dfrac{\pi}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(6x-\dfrac{\pi}{2}\right)=0\\sin\left(4x+\dfrac{\pi}{2}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}6x-\dfrac{\pi}{2}=k\pi\\4x+\dfrac{\pi}{2}=k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+\dfrac{k\pi}{6}\\x=-\dfrac{\pi}{8}+\dfrac{k\pi}{4}\end{matrix}\right.\)
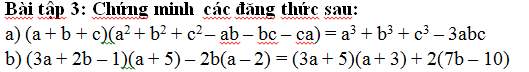
1.d
2.e
3.a
4.f
5.b
6.c