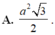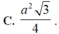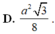cho tam giác abc cố định xét các hình chữ nhật có hai đỉnh ở trên BC và hai đỉnh kia ở trên hai cạnh còn lại của tam giác. Tìm hình chữ nhật có diện tích lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
27 tháng 12 2017
Em có thể tham khảo tại đây nhé.
Câu hỏi của Nguyễn Tuấn Minh - Toán lớp 8 - Học toán với OnlineMath
CH
Cô Hoàng Huyền
Admin
VIP
27 tháng 12 2017
Gọi AH là đường cao của tam giác ABC.
Gọi MNPQ là hình chữ nhật thỏa mãn điều kiện đề bài. Gọi O là tâm hình chữ nhật MNPQ.
Gọi E, F, D, G lần lượt là trung điểm của QM, PN, AH và BC. Khi đó O là trung điểm EF.
Gọi F' là giao điểm của PN và CD. Áp dụng định lý Talet ta có:
\(\frac{PF'}{AD}=\frac{FC}{CD}=\frac{F'N}{DH}\) mà AD = DH nên PF' = F'N hay F' là trung điểm của PN. Vậy F' trùng F hay F thuộc DC. Tương tự E thuộc DB.
Gọi O' là giao điểm của EF với DG. Áp dụng định lý Ta let ta có:
\(\frac{EO'}{BG}=\frac{DO'}{DG}=\frac{O'F}{GC}\) mà BG = GC nên EO' = O'F hay O' là trung điểm EF.
Từ đó suy ra O' trùng O hay O thuộc DG. Do A, B, C cố định nên DG cố định,.
Vậy tâm hình chữ nhật luôn nằm trên đoạn thẳng DG.
CH
Cô Hoàng Huyền
Admin
VIP
27 tháng 12 2017
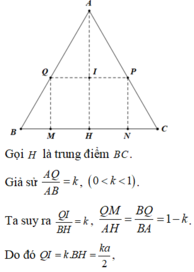
a) Đặt tên các điểm như hình vẽ.
Giả sử BC = a; BM = x. Ta có MN = QP = a - 2x
Áp dụng định lý Ta let ta có:
\(\frac{AQ}{AB}=\frac{QP}{BC}\Rightarrow AQ=\frac{AB.QP}{BC}=a-2x\)
\(\Rightarrow QB=AB-AQ=a-\left(a-2x\right)=2x\)
\(\Rightarrow QM=\sqrt{QB^2-BM^2}=\sqrt{4x^2-x^2}=x\sqrt{3}\)
\(\Rightarrow S_{MNPQ}=MN.QM=\left(a-2x\right).x\sqrt{3}\)
\(=-2\sqrt{3}x^2+a\sqrt{3}x\)
\(=-2\sqrt{3}\left(x^2-2.\frac{a}{4}.x+\frac{a^2}{16}\right)+\frac{a^2\sqrt{3}}{8}\)
\(=-2\sqrt{3}\left(x-\frac{a}{4}\right)^2+\frac{a^2\sqrt{3}}{8}\le\frac{a^2\sqrt{3}}{8}\)
Vậy diện tích lớn nhất của hình chữ nhật là \(\frac{a^2\sqrt{3}}{8}\) khi BM = BC/4
b) Em tham khảo tại đây nhé.
Câu hỏi của Nguyễn Tuấn Minh - Toán lớp 8 - Học toán với OnlineMath