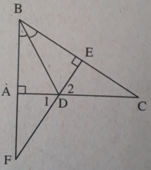
Tam giác ABC vuông tại A , phân giác BD kẻ DE vuông với BC ( E thuộc BC ) Gọi F là giao điểm của BA và ED . cm
a) BD là đường trung trực của AE
b)cm DF=DC
c) cm AD < DC
vẽ hình giùm lun nghe
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trực của AE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
=>ΔDAF=ΔDEC
=>DF=DC
c: AD=DE
DE<DC
=>AD<DC

a: Xet ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trựccủa AE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=gócEDC
=>ΔDAF=ΔDEC
=>DF=DC
c: AD=DE
mà DE<DC
nên AD<DC
d: Xet ΔBFC có BA/AF=BE/EC
nên AE//CF

(a) Xét \(\Delta ABD,\Delta EBD:\left\{{}\begin{matrix}\hat{BAD}=\hat{BED}=90^o\left(gt\right)\\\text{BD chung}\\\hat{EBD}=\hat{ABD}\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABD=\Delta EBD\left(c.h-g.n\right)\Rightarrow\left\{{}\begin{matrix}BA=BE\\DA=DE\end{matrix}\right.\)
\(\Rightarrow BD\) là đường trung trực của \(AE\left(đpcm\right).\)
(b) Xét \(\Delta ADF,\Delta EDC:\left\{{}\begin{matrix}\hat{DAF}=\hat{DEC}=90^o\left(gt\right)\\AD=DE\left(cmt\right)\\\hat{ADF}=\hat{EDC}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ADF=\Delta EDC\left(g.c.g\right)\Rightarrow AF=CE.\)
Lại có: \(BA=BE\left(cmt\right)\Rightarrow BA+AF=BE+CE\Leftrightarrow BC=BF\)
\(\Rightarrow\Delta BCF\) cân tại \(B.\)
Ta cũng có: \(\left\{{}\begin{matrix}FE\perp BC\\CA\perp BF\\FE\cap CA=\left\{D\right\}\end{matrix}\right.\Rightarrow BD\) là đường cao thứ ba của \(\Delta BCF\Rightarrow BD\) vừa là đường cao, vừa là đường trung trực của \(CF\Rightarrow DC=DF\left(đpcm\right).\)

Bạn tự vẽ hình nha!!!
a. Sorry!!!
b.
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (cạnh huyền - góc nhọn)
=> AD = ED (2 cạnh tương ứng) => D thuộc đường trung trực của AE
AB = EB (2 cạnh tương ứng) => B thuộc đường trung trực của AE
=> BD là đường trung trực của AE
c.
Xét tam giác AFD và tam giác ECD có:
DEC = DAF ( = 90 )
AD = ED (tam giác ABD = tam giác EBD)
ADF = EDC (2 góc đối đỉnh)
=> Tam giác AFD = Tam giác ECD (g.c.g)
=> DF = DC (2 cạnh tương ứng)
d.
Tam giác EDC vuông tại E
=> DC > DE (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mad DE = DA (tam giác ABD = tam giác EBD)
=> DC > DA

Xét ΔABD và ΔEBD có:
BD chung
∠ABD = ∠EBD ( do BD ,là tia phân giác của góc ABC )
∠BAD = ∠BED = 90º
Suy ra: ΔABD = ΔEBD (cạnh huyền – góc nhọn) ⇒ BA = BE, DA = DE.
Do BA = BE nên B thuộc đường trung trực của AE.
Do DA = DE nên D thuộc đường trung trực của AE.
Do đó BD là đường trung trực của AE.

a, Xét tam giác ABD và tam giác EBD có:
góc BAD=BED(tam giác abc vuông, DE vuông góc BC)
BD=BD(chung)
góc ABD=EBD (BD là phân giác)
=)tam giác ABD=tam giác EBD(cạnh huyền-góc nhọn)
vậy.....
b,gọi giao của AE và BD là O
ta có tam giác ABD=tam giác EBD
=)AB=BE ( 2 cạnh tưng ứng)
xét tam giác ABO và tam giác EBO có:
AB=BE (cmt)
góc ABO=EBO ( BD là phân giác)
BO=BO ( chung)
=)tam giác ABO=EBO (c-g-c)
=)AO=OE ( 2 cạnh tương ứng)(1)
AOB=EOB( 2 góc tương ứng)
mà AOB+EOB=180 độ ( 2 góc kề bù)
=)AOB=EOB=180:2=90độ
=)BO vuông góc AE (2)
từ(1) và (2)=)BO là trung trực AE
vậy....
c, Ta có tam giác DEC vuông tại E
=)DC>DE ( trong tam giác vuông cạnh huyền là cạnh lớn nhất)
mà DE=DA ( tam giác ABD= tam giác EBD)
=)DC>DA
hay DA<DC
vậy....
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔBAD=ΔBED
nên BA=BE và DA=DE
Ta có: BA=BE
nên B nằm trên đường trung trực của AE\(\left(1\right)\)
Ta có: DA=DE
nên D nằm trên đường trung trực của AE\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra BD là đường trung trực của AE
xét tam giác ADB và tam giác EDB có
góc DAB = góc DEB =\(90^0\)
DB cạch chung
góc ABD=góc EBD ( BD là tia phân giác của góc B)
tam giác ADB = tam giác EBD ( cạnh huyền - góc nhọn )
suy ra AB = EB
gọi H là điểm giao nhau của AE và BD
xét tam giác AHB và tam giác EHB có
AB=BE
BH là cạnh chung
góc ABH = góc EBH ( bd là tia phân giác của góc B )
suy ra tam giác AHB = tam giác EHB ( c-g-c)
suy ra AH = HE
hay H là trung điểm của AE
suy ra góc AHB = góc EHB
mà AHB + EHB = \(180^0\)
AHB + EHB = AHB . 2 = \(180^0\)
AHB = EHB = \(180^0:2=90^0\)
suy ra BD là đường trung trực của AE
xét tam giác FAD và tam giác CED có
AD = ED ( tam giác ABD = tam giác EBD )
góc FDC = góc CDE ( hai góc đối đỉnh )
góc FAD = góc CED =\(90^0\)
Tam giác FAD = tam giác CED ( g-c-g )
suy ra DC = DF
áp dụng định lý pitago vào tam giác vuông FAD tại A
\(FD^2=FA^2+AD^2\)
mà FD , FA, AD đều lớn hơn 0
suy ra \(FD^2>AD^2\)
suy ra AD< FD
mà FD = DC
suy ra DC>AD