cho tam giác ABC vuông tại A có AC = 8, góc B = 30 độ. khi đó AB bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ trung tuyến AM, AM = 1/2 BC = MB = MC
a) Nêu góc B = 30 độ thì góc C bằng 60 độ
Tam giác MAC cân tại M có góc C bằng 60 độ nên nó là tam giác đều => AC = MC = 1/2 BC
b) Nếu AC = 1/2 BC => Tam giác MAC đều vì AC = 1/2 BC = MC = MA
=> Góc C bằng 60 độ
Trong tam giác ABC có góc A = 90 độ, góc C = 60 độ => góc B = 30 độ

a: BC=10cm
C=AB+BC+AC=6+8+10=24(cm)
b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
c: Ta có: ΔABD=ΔHBD
nên DA=DH
mà DH<DC
nên DA<DC


Ta có: \(cos\left(B\right)=\dfrac{AB}{BC}\)
\(\Rightarrow cos\left(30^o\right)=\dfrac{AB}{8}\Rightarrow AB=cos\left(30^o\right)\cdot8\approx6,9\left(cm\right)\)
Ta có tam giác ABC vuông tại A áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{BC^2-AC^2}=\sqrt{8^2-6,9^2}\approx4\left(cm\right)\)

3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)

ΔABC vuông tại A
=>BC^2=AB^2+AC^2
=>BC^2=6^2+8^2=100
=>BC=10(cm)
Xét ΔBAC có BD là phân giác
nên DA/AB=DC/BC
=>DA/3=DC/5
=>\(\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{AC}{8}=1\)
=>DC=5(cm)
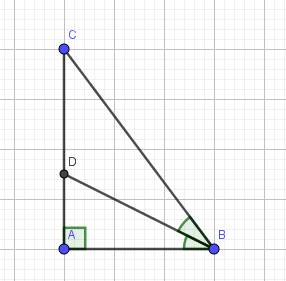
\(\Delta ABC\) vuông tại A
\(\Rightarrow BC^2=AB^2+AC^2\) (Pytago)
\(=6^2+8^2\)
\(=100\)
\(\Rightarrow BC=10\left(cm\right)\)
Do BD là tia phân giác của \(\widehat{ABC}\)
\(\Rightarrow\dfrac{AB}{AD}=\dfrac{BC}{DC}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{AB}{AD}=\dfrac{BC}{DC}=\dfrac{AB+BC}{AD+DC}=\dfrac{6+10}{8}=2\)
\(\dfrac{BC}{DC}=2\Rightarrow DC=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)

a: BC=căn 6^2+8^2=10cm
BH=AB^2/BC=3,6cm
CH=10-3,6=6,4cm
sin ABC=AC/BC=4/5
=>góc ABC=53 độ
b: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
c: góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật
góc KAC+góc AFE
=góc AHE+góc KCA
=góc ABC+góc ACB=90 độ
=>AK vuông góc EF

\(AB=\dfrac{AC}{\tan B}=\dfrac{8}{\tan30^0}=\dfrac{8}{\dfrac{\sqrt{3}}{3}}=8\sqrt{3}\)
trên tia đối tia AC lấy điểm D sao cho AD=AC
tam giác ABD =tam giác ABC(c.g.c) =>BD=BC
tam giác BDC cân có góc C=60 độ (A=90 do;B=30do)nen la tam giac deu
Do đó BC=DC =2AC=>AC=BC :2=4cm