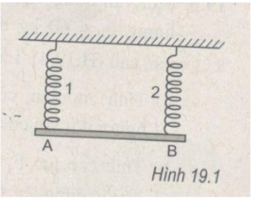
Một người dùng một thanh cứng dài để treo hai túi hàng. Một túi nặng 40 kg treo ở 1 đầu của thanh cách điểm tựa 60 cm. Hỏi phải đặt treo túi thứ hai nặng 60kg cách điểm tựa bao nhiêu để thanh cân bằng nằm ngang. Bỏ qua trọng lượng của thanh.Giúp em với ạ :(((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi d1 là khoảng cách từ thúng gạo đến vai, với lực P1
d2 là khoảng cách từ thúng ngô đến vai, với lực P2
P1.d1 = P2.d2 ↔ 300d1 = ( 1,5 – d1).200
→ d1 = 0,6m → d2 = 0,9m
F = P1 + P2 = 500N.
dữ liệu này bạn lấy ở đâu vậy nó có khớp với bài của mk đâu

Chọn A.
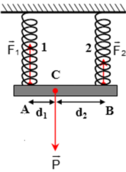
Thanh chịu ba lực song song cân bằng. Muốn cho thanh vẫn nằm ngang thì hai lò xo phải dãn ra như nhau.
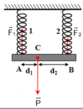
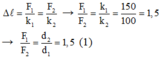
Lại có: d1 + d2 = 75 (2)
Từ (1) và (2) → d1 = CA = 30 cm, d2 = CB = 45 cm.

Chọn B.
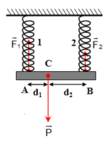
Thanh chịu ba lực song song cân bằng. Muốn cho thanh vẫn nằm ngang thì hai lò xo phải dãn ra như nhau.
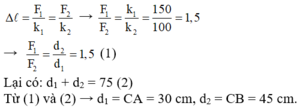

Bài 1.
a)\(OA=40cm\Rightarrow OB=160-40=120cm\)
Theo hệ cân bằng của đòn bẩy:
\(F_1\cdot l_1=F_2\cdot l_2\)
\(\Rightarrow\dfrac{F_1}{F_2}=\dfrac{l_2}{l_1}=\dfrac{OB}{OA}=\dfrac{120}{40}=3\)
\(\Rightarrow F_2=\dfrac{F_1}{3}=\dfrac{P_1}{3}=\dfrac{10m_1}{3}=\dfrac{10\cdot9}{3}=30N\)
\(\Rightarrow m_2=\dfrac{P_2}{10}=\dfrac{F_2}{10}=\dfrac{30}{10}=3kg\)
b)Vật \(m_2\) giữ nguyên không đổi. \(\Rightarrow F_2=P_2=30N\)
\(OB'=60cm\Rightarrow OA'=160-60=100cm\)
Theo hệ cân bằng của đòn bẩy:
\(F_1'\cdot l_1'=F_2\cdot l_2'\)
\(\Rightarrow F_1'=\dfrac{F_2\cdot l_2'}{l_1'}=\dfrac{30\cdot60}{100}=18N\) \(\Rightarrow m_1'=1,8kg\)
Mà \(m_1=9kg\)
\(\Rightarrow\) Phải giảm vật đi một lượng là:
\(\Delta m=m_1-m_1'=9-1,8=7,2kg\)
Bài 2.
a)Áp dụng hệ cân bằng của đòn bẩy:
\(\dfrac{F_1}{F_2}=\dfrac{OA}{OB}=\dfrac{10m_1}{10m_2}=\dfrac{6}{4}=\dfrac{3}{2}\)
\(\Rightarrow2OA=3OB\left(1\right)\)
Mà \(OA+OB=120\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) \(\Rightarrow\left\{{}\begin{matrix}OA=72cm\\OB=48cm\end{matrix}\right.\)
Vậy O nằm cách A và B lần lượt một đoạn là 72cm và 48cm.
b)Giữ nguyên vật 2 \(\Rightarrow F_2=P_2=10m_2=40N\)
Tăng khối lượng \(m_1\) lên 2kg thì \(F_1=P_1=10\cdot\left(2+6\right)=80N\)
Để thanh AB nằm cân bằng:
\(F_1\cdot OA'=F_2\cdot OB'\)
\(\Rightarrow\dfrac{F_1}{F_2}=\dfrac{OB'}{OA'}=\dfrac{80}{40}=2\)
\(\Rightarrow OB'=2OA'\left(1\right)\)
Mà \(OA'+OB'=120\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) \(\Rightarrow\left\{{}\begin{matrix}OA'=40cm\\OB'=80cm\end{matrix}\right.\)
Vậy O nằm trên AB cách A và B lần lượt là 40cm và 80 cm.