Cho đường tròn tâm O, điểm M nằm bên ngoài đường tròn, kẻ các tiếp tuyến MB, MA (A,B là các tiếp điểm)
a) Chứng minh OM là đường trung tuyến của tam giác MAB
b) Tính độ dài các cạnh của tam giác MAB, biết AO= 3
Mong các cao nhân trợ giúp :>>>
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 8 2021
a: Xét (O) có
MA là tiếp tuyến có A là tiếp điểm
MB là tiếp tuyến có B là tiếp điểm
Do đó: MA=MB
Ta có: IA=IB
nên I nằm trên đường trung trực của AB(1)
ta có: MA=MB
nên M nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra IM là đường trung trực của AB
hay IM\(\perp\)AB
b: Xét (I) có
ΔABE nội tiếp đường tròn
BE là đường kính
Do đó: ΔABE vuông tại A
Ta có: BA\(\perp\)IM
BA\(\perp\)AE
Do đó: AE//MI
CM
28 tháng 11 2018
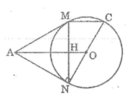
Ta có: AN ⊥ NC (tính chất tiếp tuyến)
Áp dụng định lí Pitago vào tam giác vuông AON ta có :
A O 2 = A N 2 + O N 2
Suy ra : A N 2 = A O 2 - O N 2 = 5 2 - 3 2 = 16
AN = 4 (cm)
Suy ra: AM = AN = 4 (cm)
Gọi H là giao điểm của AO và MN
Ta có: MH = NH = MN/2 (tính chất tam giác cân)
Tam giác AON vuông tại N có NH ⊥ AO. Theo hệ thức lượng trong tam giác vuông, ta có:
OA.NH = AN.ON ⇒ NH = (AN.ON)/AO = (4.3)/5 = 2,4 (cm)
MN = 2.NH = 2.2,4 = 4,8 (cm)
10 tháng 11 2021
Bài 2:
(Bạn vẽ hình thì vẽ nửa trên đường thôi nha, tại đề cho là nửa đường tròn tâm O)
a, Vì AC//BD (⊥AB) nên ABDC là hthang
Mà \(\widehat{CAB}=90^0\) nên ABDC là hthang vuông
b, Gọi I là trung điểm CD
Mà O là trung điểm AB nên OI là đtb hthang ABDC
Do đó OI//AC\(\Rightarrow\)OI⊥AB
Mà tam giác OCD vuông tại O nên OI là bán kính đg tròn ngoại tiếp tam giác OCD
Do đó AB là tiếp tuyến tại O của (I)
Vậy đường tròn ngoại tiếp tam giác COD tiếp xúc với đường thẳng AB tại O.
c, Kẻ OH⊥CD
Vì \(\widehat{AOC}=\widehat{IOD}\) (cùng phụ \(\widehat{COI}\)), \(\widehat{IOD}=\widehat{IDO}\left(IO=ID=\dfrac{1}{2}CD\right)\) nên \(\widehat{AOC}=\widehat{IDO}\Rightarrow90^0-\widehat{AOC}=90^0-\widehat{IDO}\Rightarrow\widehat{ACO}=\widehat{HCO}\)
Vì \(\left\{{}\begin{matrix}\widehat{ACO}=\widehat{HCO}\\CO.chung\\\widehat{CAO}=\widehat{CHO}=90^0\end{matrix}\right.\) nên \(\Delta AOC=\Delta HOC\Rightarrow OA=OH\Rightarrow H\in\left(O\right)\)
Mà CD⊥OH nên CD là tt tại H của (O)
Do đó \(CA\cdot DB=CH\cdot HD=OH^2=R^2\) (kết hợp HTL)
7 tháng 11 2021
a: Xét ΔOAM vuông tại A có
\(OM^2=OA^2+AM^2\)
hay \(AM=5\sqrt{3}\left(cm\right)\)
CM
16 tháng 6 2018
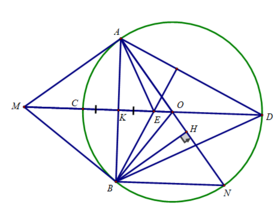
d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB
6 tháng 1 2023
a: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
=>ΔABC cân tại A
b: OB=OC
AB=AC
Do đó: AO là trung trực của BC
=>AO vuông góc với BC