đởn giản các biểu thức sau
sin a.cos a.cos2a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


... \(=\left(sin^2a\right)^2+2\cdot sin^2a\cdot cos^2+\left(cos^2a\right)^2=\left(sin^2a+cos^2a\right)^2=1^2=1\)

Chọn A.
Ta có: A= cos2( x-a) + cos2x -2cos a.cos x.cos( a - x).
= cos( x - a) [ cos(x - a) – 2cosa. cosx] + cos2x
= cos( x - a) [ cos x.cosa + sina.sinx – 2cosa.cosx] + cos2x
= cos( x - a) [ -cos x.cosa + sina.sinx] + cos2x
= -cos( x - a) .cos( x + a) + cos2x

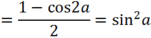


Mình bấm máy tính cho nhanh
ta có tan a =2
suy ra a=63,4349488
gán x=a= cái số ở trên
Sau đó Bấm biểu thức A mà thay a là x đó
ta được A=1

a) \(A=sin\left(90^0-x\right)+cos\left(180^0-x\right)+sin^2x\left(1+tan^2x\right)-tan^2x\)
\(=cosx-cosx+sin^2x.\left(\dfrac{1}{cos^2x}\right)-tan^2x\)
\(=tan^2x-tan^2x\)
\(=0\)
b) \(B=\dfrac{1}{sinx}.\sqrt{\dfrac{1}{1+cosx}+\dfrac{1}{1-cosx}}-\sqrt{2}\)
\(=\dfrac{1}{sinx}.\sqrt{\dfrac{1-cosx+1+cosx}{1-cos^2x}}-\sqrt{2}\)
\(=\dfrac{1}{sinx}.\sqrt{\dfrac{2}{sin^2x}}-\sqrt{2}\)
\(=\dfrac{\sqrt{2}}{sin^2x}-\sqrt{2}\)
\(=\dfrac{\sqrt{2}\left(1-sin^2x\right)}{sin^2x}\)
\(=\dfrac{\sqrt{2}cos^2x}{sin^2x}\)
\(=\sqrt{2}tan^2x\)

Lần sau đăng đề bạn nên gõ công thức cho gọn, đừng đăng ảnh dài oạch như thế này nhìn rất khó.
Lời giải:
Ta có:
\(x^2=\frac{1}{4}(\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}})^2=\frac{1}{4}(\frac{a}{b}+\frac{b}{a}+2)\)
\(\Rightarrow x^2-1=\frac{1}{4}(\frac{a}{b}+\frac{b}{a}-2)=\frac{1}{4}(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})^2\)
\(\Rightarrow \sqrt{x^2-1}=\frac{1}{2}|\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}}|=\frac{1}{2}(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})\)
Do đó:
\(2b\sqrt{x^2-1}=b.\frac{a-b}{\sqrt{ab}}=(a-b).\sqrt{\frac{b}{a}}\)
\(x-\sqrt{x^2-1}=\frac{1}{2}[\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}}-(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})]\)
\(=\sqrt{\frac{b}{a}}\)
$\Rightarrow B=a-b$

t g 2 α - sin 2 α . t g 2 α = t g 2 α ( 1 - sin 2 α ) = t g 2 α sin 2 α + c o s 2 α - sin 2 α = t g 2 α . c o s 2 α = sin 2 α / c o s 2 α . c o s 2 α = sin 2 α
sinacosacos2a =( sin2a.cos2a)/2 =( sin4a)/4