Diện tích của một hình thoi là 540dm2. Một trong những đường chéo của nó bằng 4,5dm. Tính khoảng cách giao điểm của các đường chéo đến các cạnh.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 8 2018
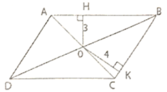
Ta có: SABCD = 2.0H.AB = 2.3.AB = 6AB
Mà SABCD = 48cm2
Suy ra 6AB = 48 => AB = 8(cm)
Mặt khác: 2OK.BC = SABCD => 2.4.BC = 48 => BC = 6(cm)
Chu vi hình bình hành ABCD là (8 + 6).2 = 28 (cm)
21 tháng 9 2016
k/c = 1/2 dg chéo => k/c do la dg trung bình nên cạnh ben = dg cheo còn lai
tu do cac góc cua hình thoi la 60 va 120
bn vẽ hình ra la thay liền
CM
14 tháng 8 2017
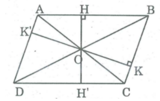
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2cm , đến cạnh BC là OK = 3cm
* Kéo dài OH cắt cạnh CD tại H'.
Ta có OH ⊥ BC
⇒ OH' ⊥ CD và OH' = 2cm
Suy ra HH' bằng đường cao của hình bình hành.
S
A
B
C
D
= HH'.AB ⇒ 
* Kéo dài OK cắt AD tại K'.
Ta có: OK ⊥ BC ⇒ OK' ⊥ CD và OK' = 3 (cm)
Suy ra KK' là đường cao của hình bình hành.
S
A
B
C
D
= KK'.AB ⇒ 
Chu vi của hình bình hành ABCD là (6 + 4).2 = 20 (cm).
19 tháng 1 2022
Gọi độ dài đường chéo thứ nhất là x
Độ dài đường chéo thứ hai là 34-x
Theo đề, ta có: x(34-x)=240
\(\Leftrightarrow34x-x^2-240=0\)
\(\Leftrightarrow x^2-34x+240=0\)
\(\Leftrightarrow\left(x-10\right)\left(x-24\right)=0\)
=>x=10 hoặc x=24
Vậy: Độ dài cạnh là \(\sqrt{\left(\dfrac{10}{2}\right)^2+\left(\dfrac{24}{2}\right)^2}=\sqrt{5^2+12^2}=13\left(m\right)\)
H9
HT.Phong (9A5)
CTVHS
27 tháng 3 2023
Diện tích của hình vuông: \(5\times5=25\left(dm^2\right)\)
Chiều dài đường chéo còn lại: \(25\times2:5=10\left(dm\right)\)