đồ thị của hàm số y=x^2-2x-3 có trục đối xứng là đường thẳng có phương trình
A.y=x^2
B.y=x^4
C.y=x^3
D.y |x|
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Theo đề, ta có:
-b/2*(-1)=5/2
=>-b/-2=5/2
=>b=5
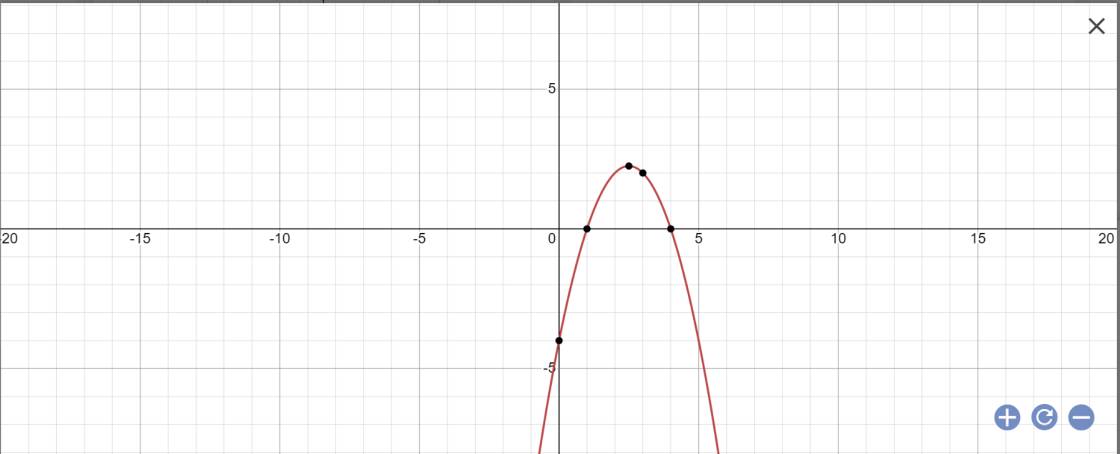
2: y=-x^2+5x-4

Đáp án :
B. Đồ thị hàm số chẵn nhận trục hoành làm trục đối xứng.

1) Hai đồ thị gọi là đối xứng với nhau qua trục hoành nếu f(x)+f(x)'=0
Do:
f(x)=x-2,f(x)'=2-x và f(x)+f(x)'=0=>Chúng đối xứng với nhau qua trục hoành.

Đáp án A
Ta đưa hàm số về dạng: y = 5 x 2 = 5 x .
Dựa vào lý thuyết “Hai hàm số y = a x , y = log a x có đồ thị đối xứng nhau qua đường phân giác của góc phần tư thứ nhất y = x”
Hoặc thay x = y và y = x ta có x = 5 y ⇔ y = log 5 x
Lỗi sai:
Có bạn sẽ chọn B vì x = 5 y 2 ⇔ y 2 = log 5 x ⇔ y = 2 log 5 x = log 5 x 2
Hai hàm số y = a x , y = log a x có đồ thị đối xứng nhau qua đường phân giác của góc phần tư thứ nhất y = x.

Do đường thẳng có hệ số góc bằng 5 nên loại D
Thay tọa độ N vào 3 đáp án A, B, C chỉ có B thỏa mãn
Vậy B là đáp án đúng

Thay \(x=0;y=3\Leftrightarrow c=3\Leftrightarrow\left(P\right):y=ax^2-x+3\)
Vì (P) có trục đx là \(\dfrac{1}{2}\Leftrightarrow-\dfrac{\left(-1\right)}{a}=\dfrac{1}{2}\Leftrightarrow a=2\)
Vậy \(\left(P\right):y=2x^2-x+3\)

Gọi công thức của hàm số bậc hai là \(y=ax^2+bx+c\)
Trục đối xứng là x=3 nên \(-\dfrac{b}{2a}=3\)
=>b=-2a
Thay x=0 và y=-16 vào (d), ta được:
\(a\cdot0^2+b\cdot0+c=-16\)
=>c=-16
=>\(y=ax^2+bx-16\)
Thay x=-2 và y=0 vào (d), ta được:
\(a\cdot\left(-2\right)^2+b\left(-2\right)-16=0\)
=>4a-2b-16=0
=>\(4a-2\cdot\left(-2a\right)=16\)
=>8a=16
=>a=2
=>b=-2a=-4
Vậy: Công thức cần tìm là \(y=2x^2-4x-16\)
Chọn A
cho em hỏi sao không phải đáp án B ạ ???