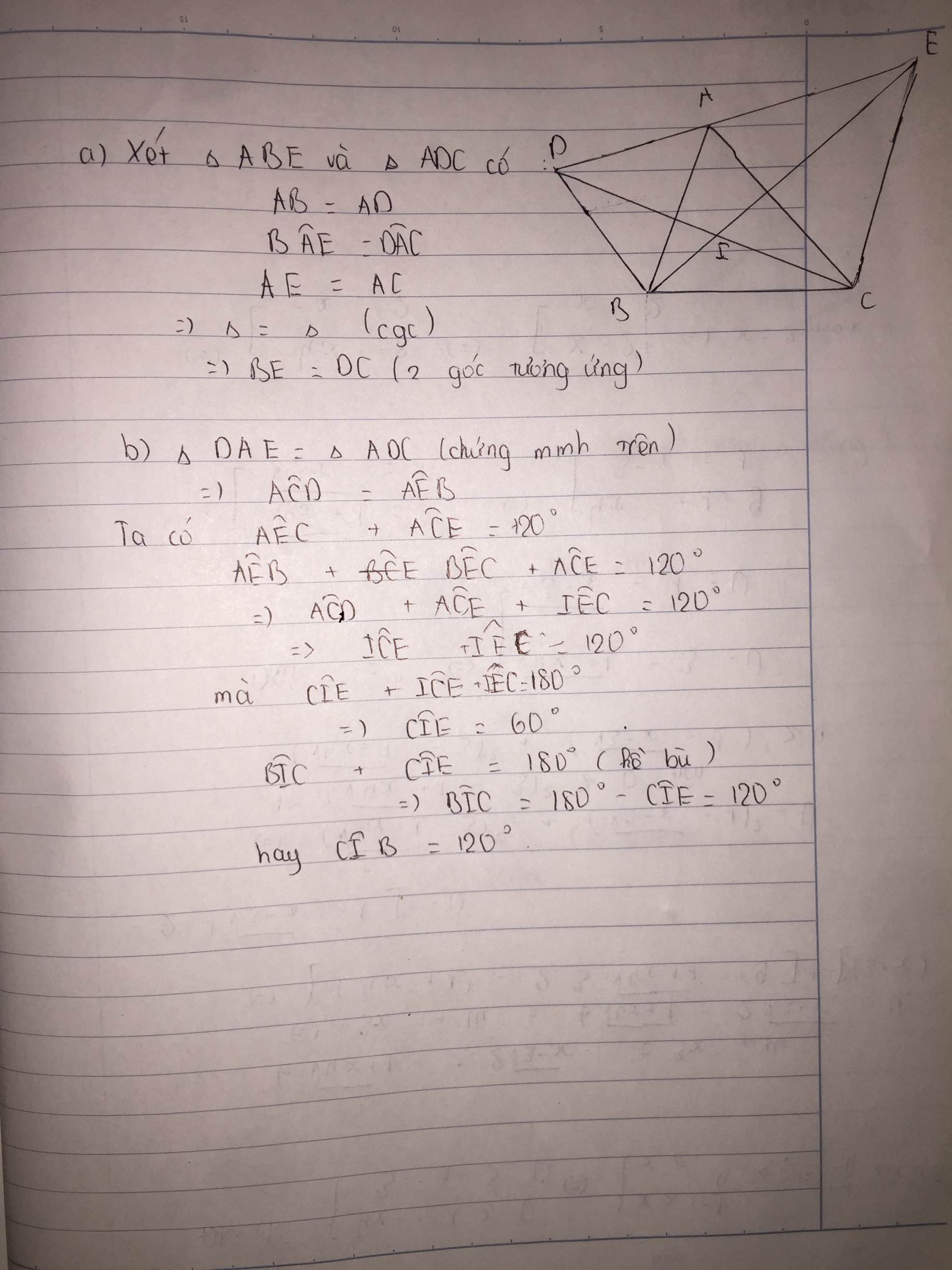Cho tam giác ABC, về phía ngoài tam giác dựng các tam giác ABD và ACE vuông cân tại A. BE cắt CD tại I. Vậy góc BIC=?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 2 2017
Hình thì bạn tự vẽ nha: a,Do tam giác ABC là tam giác cân góc ABC=góc ACB(1)
Lại có tam giác ABD và tam giác ACE là 2 tam giác cân,AB=AC(giả thiết)
tam giác ABD=tam giác ACE
góc DBA=góc ECA(2)
Từ (1) và (2) góc DBA+ góc ABC= góc ACE+ góc ACB Hay góc DBC=góc ECB
Xét tam giác DBC và tam giác CEB:
Tam giác ABD=tam giác ACE(chứng minh trên),và là 2 tam giác cân DB=CE
Góc DBC=góc ECB(chứng minh trên)
Chung BC
tam giác DBC=tam giác CBE
AL
24 tháng 1 2018
Gọi F là giao điểm của AB và CD
Xét tam giác ADC và tam giác ABE có
AD=AB,góc BAC= góc BAE(=60 +90),AC=AE
=>Tam giác ADC= tam giác ABE=> góc ADC= góc ABE
Xét tam giac ADF và tam giác FBI có
góc ADF= góc FBI, góc AFD= góc BFI=>\(\widehat{DAF=\widehat{FIB}}\)=90
mà \(\widehat{BIC}\)\(=180-\widehat{FIB}\Rightarrow\widehat{BIC}=180-90=90\)
10 tháng 3 2023
a: Xet ΔBAE và ΔDAC có
BA=DA
góc BAE=góc DAC(=150 độ)
AE=AC
=>ΔBAE=ΔDAC
=>BE=DC
b: Gọi F là giao của AB và CD
Xét ΔADF và ΔIBF có
goc ADF=góc FBI
góc AFD=góc BFI
=>ΔADF đồng dạng với ΔFBI
=>góc DAF=góc BIF=60 độ
=>góc BIC=120 độ
10 tháng 3 2023
Sửa đề: vuông cân tại A
a: Xét ΔADC và ΔABE có
AD=AB
góc DAC=góc BAE
AC=AE
=>ΔADC=ΔABE
=>DC=EB
b: AD vuông góc AC
AE vuông góc AB
góc ADC=góc ABE
=>EB vuông góc CD
