Câu hỏi: Từ các số 1, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 3 chữ số chia hết cho 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 1 2018
GỌI ABCD LÀ CÁC SỐ TN CẦN TÌM
TA CÓ ABCD\(⋮\)5
=>D\(\in\)(0;5)
NẾU D=0
=> ABCD=1350;1370;1390;1530;1730;1930;1950;1970;1790;1750;1570;1590;...
CÓ TẤT CẢ 60 SỐ CHIA HẾT CHO 5
NẾU D=5
=>ABCD=1305;1035;1795;1975;1075;1705;1375;1735;1905;1095;1935;1395;...
CÓ TẤT CẢ 48 SỐ CHIA HẾT CHO 5
VẬY TỪ CÁC SỐ 0;1;3;5;7;9 CÓ THỂ LẬP ĐC 108 SỐ CHIA HẾT CHO 5
CM
2 tháng 1 2018
Sơ đồ con đường |
Lời giải chi tiết |
|
Gọi số có 3 chữ số chia hết cho 3 là a b c - . Khi đó tổng các chữ số là a+b+c chia hết cho 3. Các bộ 3 số thoã mãn điều kiện đó là: 1 ; 3 ; 5 , 1 ; 5 ; 6 , 3 ; 4 ; 5 , 4 ; 5 ; 6 Mỗi bộ 3 lại có: 3 cách chọn hàng trăm. 2 cách chọn hàng chục. 1 cách chọn hàng đơn vị. Có: 3.2.1= 6 cách chọn. Vậy tổng có: 4.6= 24 cách chọn. |
CM
25 tháng 9 2019
Sơ đồ con đường |
Lời giải chi tiết |
|
Gọi số cần lập có dạng a b c ¯ .
Từ a b c ¯ ⋮ 5 ⇒ c = 5 , ta có a b 5 ¯ . Từ a b 5 ¯ ⋮ 3 ⇒ a + b + 5 ⋮ 3 suy ra tồn tại những cặp a ; b là 1 ; 3 ; 1 ; 6 ; 3 ; 4 ; 4 ; 6 Hơn nữa, a và b bình đẳng nên có tổng cộng: 4.2=8 số tìm được. |
CM
20 tháng 10 2019
Đáp án A
Gọi số cần tìm là 
. Số mà chia hết cho 
thì phải chia hết cho 3 và 5.
Trường hợp 1. Số cần tìm có dạng 
, để chia hết cho 
thì a, b, c, d phải thuộc các tập sau 
Do đó trong trường hợp này có 
số.
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
Việc lập số tự nhiên gồm ba chữ số chia hết cho 5 là thực hiện 3 hành động liên tiếp: chọn chữ số hàng đơn vị, chọn chữ số hàng chục, chọn chữ số hàng trăm.
chọn chữ số hàng đơn vị: Có 1 cách chọn (số 5).
chọn chữ số hàng chục: Có 6 cách chọn.
chọn chữ số hàng trăm: Có 6 cách chọn.
Theo quy tắc nhân, số số tự nhiên lập được là: 1.6.6=36 (số).
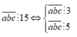
Gọi số cần tìm là abc
Số chia hết cho 5⇒ c =5 ⇒ c có 1 cách
a có 6 cách, b có 6 cách
⇒ có 1.6.6=36 cách