Một máy bay đang bay ngang với tốc độ 180 m/s ở độ cao 490m thì thả 1 gói hàng, lấy g = 9, 8 m/s ^ 2 a. Gói hàng sẽ bay theo quĩ đạo nào? Sau bao lâu gói hàng rơi chạm đất? b. Tầm bay xa của gói hàng là bao nhiêu? Xác định độ lớn vận tốc của gói hàng ngay trước khi chạm đất?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
26 tháng 7 2018
Gọi v 0 là tốc độ của gói hàng khi rời khỏi máy bay. Ta có:
L m a x = v 0 t = 150.10 = 1500 m.
PL
14 tháng 12 2021
Vì khi thả gói hàng, cả máy bay cả hàng đang có vận tốc nên gói hàng sẽ chuyển động theo quán tính => Gói hàng chuyển động ném ngang.
a) Thời gian để gói hàng rơi xuống đất là: 
b) Gọi v0 là tốc độ của gói hàng khi rời khỏi máy bay.
Tầm bay xa của gói hàng là: Lmax = v0t = 150.10 = 1500 m.
c. Quỹ đạo là một phần của parabol.
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Gắn hệ trục tọa độ Oxy như hình dưới:
Gọi A vị trí hàng rơi xuống, khi đó \({y_A} = 0\). Ta có, tọa độ của A thỏa mãn:
\(\left\{ \begin{array}{l}x = 50t\\y = 80 - \frac{1}{2}.9,8.{t^2}\end{array} \right.\)
Mà \({y_A} = 0 \Rightarrow 0 = 80 - \frac{1}{2}.9,8.{t^2} \Leftrightarrow {t^2} \approx 16,33 \Rightarrow t \approx 4(s)\)
Do đó \({x_A} = 50.4 = 200(m)\) hay khoảng cách giữa máy bay và thùng hàng cứu trợ là 200m.
Vậy để thùng hàng cứu trợ rơi đúng vị trí được chọn thì máy bay cần thả hàng khi cách điểm đó 200m.
18 tháng 11 2019
2)v0=150m/s
h =490m
g=9,8m/s2
L=?
GIẢI :
Thời gian rơi của gói hàng :
\(t=\sqrt{\frac{2.490}{9,8}}=10\left(s\right)\)
Tầm xa của gói hàng là:
\(L=v_0t=150.10=1500\left(m\right)\)
18 tháng 11 2019
1) h =80m, v=50m/s; v0 =?
GIẢI :
Lấy g =10m/s2
Thời gian rơi là :
\(t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2.80}{10}}=4\left(s\right)\)
Ta có công thức : \(v=\sqrt{v_0^2+\left(gt\right)^2}=\sqrt{v_0^2+\left(10.4\right)^2}\)
=> \(50=\sqrt{v_0^2+\left(10.4\right)^2}\)
=> \(v_0=30m/s\)
VT
13 tháng 8 2019
Trong trường hợp khí cầu đang bay lên thì lúc đầu vật được ném lên cao với vận tốc đầu v 0 = 4,9 m/s bằng vận tốc bay lên của khí cầu từ độ cao s và chuyển động chậm dần đều trong khoảng thời gian t 2 lên tới độ cao lớn nhất, tại đó v = 0. Khoảng thời gian t 2 được tính theo công thức:
v = v 0 – g t 2 = 0 ⇒ t 2 = 0,5 s
Sau đó vật lại rơi tự do từ độ cao lớn nhất xuống đến độ cao 300 m trong thời gian t 2 = 0,5 s, rồi tiếp tục tơi nhanh dần đều với vận tốc v 0 = 4,9 m/s từ độ cao 300 m xuống tới đất trong khoảng thời gian t 1 ≈ 7,3 s (giống như trường hợp trên).
Như vậy, khoảng thời gian chuyển động của vật sẽ bằng: t = 2 t 2 + t 1 = 2.0,5 + 7,3 = 8,3 s.
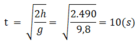
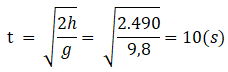
Qũy đạo bay của gói hàng: \(y=\dfrac{g}{2v_0^2}x^2\)
Thời gian rơi: \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot490}{10}}=7\sqrt{2}s\)
Tầm bay xa: \(L=v_0t=180\cdot7\sqrt{2}=1781,91m\)
Vận tốc: \(v=\sqrt{\left(gt\right)^2+v_0^2}=\sqrt{\left(10\cdot7\sqrt{2}\right)^2+180^2}=10\sqrt{422}\)m/s