cho tam giác ABC can tại A.gọi H là giao điểm các đường cao AD,BE,CF gọi I là trung điểm của BH và k là trung điểm AC.Chứng minh
a,4 điểm BDHI cùng thuộc đường trong tâm k
b a4 điểm AFDC cùng thuộc đường trong tâm k
c IK di qua trung điểm DF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 10 2021
a: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=180^0\)
Do đó: AEHF là tứ giác nội tiếp
Tâm I là trung điểm của AH
20 tháng 8 2020
Trong tam giác ABH có PK là đường trung bình nên PK//AH và \(PK=\frac{1}{2}AH\)
Trong tam giác ACH có NR là đường trung bình nên NR//AH và \(NR=\frac{1}{2}AH\)
Do đó PK//NR và PK=NR nên PNRK là hình bình hành
Mặt khác PK//AH mà AH _|_ BC => PK _|_ BC
Lại có PN //BC (do PN là đường trung bình tam giác ABC)
=> PN _|_ PK, do đó PNRK là hình chữ nhật
Gọi S là giao của PR và NK thì SP=SN=SK=SR
Chứng minh tương tự có IS=SM=SN=SK
Tam giác FPR vuông tại F có S là trung điểm PR nên SF=SP=SR
Tương tự cũng có SE=SK=SN; SD=SI=SM
=> SD=SE=SF=SM=SN=SP=SI=SK=SR
Vậy 9 điểm I,K,R,M,N,P,D,E,F cùng thuộc 1 đường tròn tâm I
Đường tròn đi qua 9 điểm được gọi là đường tròn Euler của tam giác ABC
22 tháng 11 2022
a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔDAH có DI/DH=DO/DA
nen Io//AH và IO=AH/2
=>AH=2OI
c: G là trọng tâm
nên AG=2AI
Xét ΔAHD có
AI là trung tuyến
AG=2/3AI
DO đó: G là trọng tâm
12 tháng 3 2022
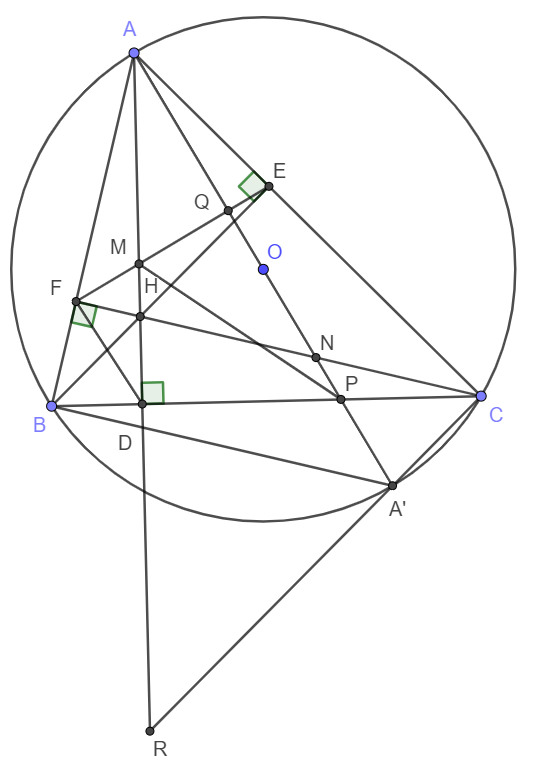
a) theo gt, BFC=BEC=90
=> BFEC nội tiếp (có 2 góc kề bang nhau)
góc AFC=ADC=90 => AFDC nội tiếp ( có 2 cạnh kề cùng nhìn một đoan thẳng bằng nhau)
b) vì tứ giác ABA'C nội tiếp => ABC = AA'C (cùng chắn cung AC)
Lại có ABC= AHF (Cùng phụ với góc BAD)
Ta thấy AFHE nội tiếp vì AFH +AEH = 90+90=180
=> AHF=AEF (Cùng chắn cung AF)
=>Đpcm
c) vì tứ giác EQA'C nôi tiếp
nên EQA'+ECA'=180 mà ECA'=90 vì là góc nội tiếp chắn nửa đường tròn
=> MQP=EQA'=90 ( vì MQP+EQA=180)
Trong đó ADC=90 =>Đpcm
d) Vì ABA'C VÀ FBDH nội tiếp nên góc NA'C=ABC=DHC
=>NA'C=DHC=>Đpcm