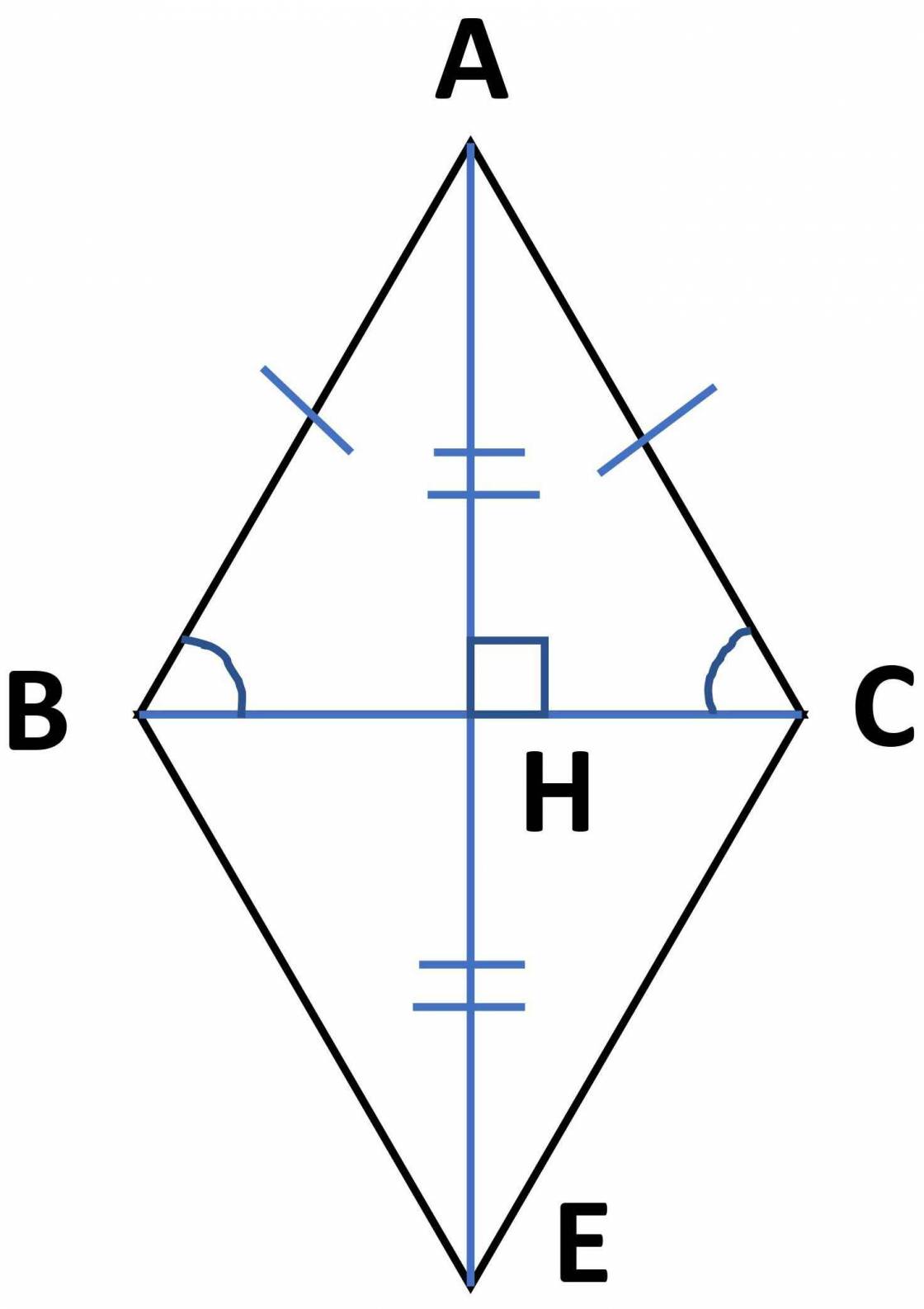
cho tam giác ABC có AB=3cm, AC=4cm, BC=5cm. AH vg góc vs BC(H thuộc BC ). Trên tia đối của HA lấy E sao cho HE=HA. CMR:
a/Tam giacsABC vg cân tại A
b/BA=BE
c/CH là tia phân giác của góc ACE
d/tam giác BEC vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 1 2022
a, Ta có :
\(AB^2+AC^2=3^2+4^2=25\)
\(BC^2=5^2=25\)
\(=> AB^2+AC^2=BC^2\)
\(=> \) △ABC vuông tại A
b, Xét △BAH và △BEH có :
\(\widehat{BHA}=\widehat{BHE}=90^o\)
BH : chung
HE = HA (GT)
=> △BAH = △BEH (c.g.c)
=> BA = BE (2 cạnh tương ứng)
c, Xét △CAH và △CEH có :
\(\widehat{CHA}=\widehat{CHE}=90^o\)
\(CH\) :chung
AH = HE (GT)
=> △CAH = △CEH (c.g.c)
=> \(\widehat{C_1}=\widehat{C_2}\)
=> CH là phân giác \(\widehat{ACE}\)
d, Xét △BAC và △BEC có :
\(BA=BE (câu a)\)
CA = CE (△CAH = △CEH)
BC : chung
=> △BAC = △BEC(c.c.c)
=> \(\widehat{BAC}=\widehat{BEC}\)
mà \(\widehat{BAC}=90^o\)
\(=> \widehat{BEC}=90^o\)
=> △BEC vuông tại E
6 tháng 3 2022
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔBAE có
BH là đường cao
BH là đường trung tuyến
DO đó:ΔBAE cân tại B
hay BA=BE
c: Xét ΔCAE có
CH là đường cao
CH là đường trung tuyến
Do đó:ΔCAE cân tại C
mà CB là đường cao
nên CB là tia phân giác của góc ACE
d: Xét ΔCAB và ΔCEB có
CA=CB
BA=BE
BC chung
DO đó:ΔCAB=ΔCEB
Suy ra: \(\widehat{CAB}=\widehat{CEB}=90^0\)
hay ΔBEC vuông tại E
GN
22 tháng 4 2018
a, áp dụng tổng 3 góc trong 1 tam giác => góc AB= 25 độ
AC < AB ( 65 độ > 25 độ)
b, Xét tam giác BHC và tam giác BHE có: BH- chung ; BHA = BHE (=90 độ) ; AH = HE ( theo đề bài)
=> hai tam giác bằng nhau (c.g.c) => BA = BE => tam giác BEA cân tại B (đpcm)
c, Dễ dàng chứng minh được tam giác BEC = tam giác BAC
=> BEC = BAC = 90 độ
=> tam giác BEC vuông tại E (đpcm)
d, Ta có: MH đi qua trung điểm của AD và AE trong tam giác ADE => NM là đường trung bình của tam giác này => MN // DE (đpcm)
20 tháng 2 2020
a.Vì AB^2 + Ac^2 = BC^2
=> Tam giác ABC vuông tại A (Py-ta-go đảo)
cậu xem lại đề bào ý b,c,d nhé. Tớ thấy nó sai sai
S
19 tháng 12 2022
a) xét ΔABH và ΔACH, ta có :
AB = AC (giả thiết)
\(\widehat{ABC}=\widehat{ACB}\) (vì AB = AC => đó là tam giác cân, mà tam giác cân thì có 2 góc ở đáy bằng nhau)
AH là cạnh chung
ð ΔABH = ΔACH (c.c.c)
b) vì ΔABH = ΔACH, nên :
=> HB = HC (2 cạnh tương ứng)
c) hơi khó nha !