Tìm các số x1; x2; x3; …; x2018. Biết rằng:
x1 + x2 + x3 + … + x2018 = 2018 và x1^3 + x2^3 + x3^3 + … + x2018^3 = x1^4 + x2^4 + x3^4 + … + x2018^4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 2 2018
Đáp án C.
Ta có y ' = 3 x 2 + 4 m − 2 x − 5 ; y ' = 0 ⇔ 3 x 2 + 4 m − 2 x − 5 = 0 (*).
Phương trình (*) có a c < 0 nên luôn có hai nghiệm trái dấu .
Suy ra x 1 = − x 1 ; x 2 = x 2 .
Khi đó x 1 , x 2 là hai điểm cực trị của hàm số.
x 1 − x 2 = − 2 ⇔ − x 1 − x 2 = − 2 ⇔ x 1 + x 2 = 2 ⇔ − 4 m − 2 3 = 2 ⇔ m = 1 2
CM
11 tháng 2 2017
Phương trình có 2 nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 13 4
⇔ a ≠ 0 Δ ≥ 0 − b a = 13 4 ⇔ m ≠ 0 m 2 − 3 3 − 4 m 2 ≥ 0 − m 2 − 3 m = 13 4
⇔ m ≠ 0 m 2 − 3 − 2 m m 2 − 3 + 2 m ≥ 0 4 m 2 + 13 m − 12 = 0
⇔ m ≠ 0 m + 1 m − 3 m − 1 m + 3 ≥ 0 m = 3 4 ; m = − 4
⇔ m ≠ 0 m ∈ − ∞ ; − 3 ∪ − 1 ; 1 ∪ 3 ; + ∞ m = 3 4 ; m = − 4 ⇔ m = 3 4 m = − 4
Vậy tổng bình phương các giá trị của m là: 265 16
Đáp án cần chọn là: A
CM
7 tháng 8 2018
Ta có y’=12x2+2mx-3.
Do ∆ ' = m 2 + 36 > 0 , ∀ m ∈ ℝ nên hàm số luôn có hai điểm cực trị x1; x2.
Theo Viet, ta có x 1 + x 2 = - m 6 x 1 x 2 = - 1 4
Mà x1+4x2=0 suy ra
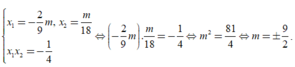
Chọn A.
15 tháng 5 2023
b: Δ=(-2m)^2-4(m^2-2m+2)
=4m^2-4m^2+8m-8=8m-8
Để pt có 2 nghiệm phân biệt thì 8m-8>0
=>m>1
x1^2+x2^2=x1+x2+8
=>(x1+x2)^2-2x1x2-(x1+x2)=8
=>(2m)^2-2(m^2-2m+2)-2m=8
=>4m^2-2m^2+4m-4-2m=8
=>2m^2+2m-12=0
=>m^2+m-6=0
=>(m+3)(m-2)=0
mà m>1
nên m=2