Cho tam giác ABC vuông tại A.Gọi G là trọng tâm của tam giác. Một đường thẳng d qua G cắt các cạnh AB, AC lần lượt tại E và F
CMR: \(\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\ge\dfrac{9}{BC^2}\)
Giúp e với ạ cảm ơn nhiều !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
Từ hình vẽ thì hướng giải như sau:
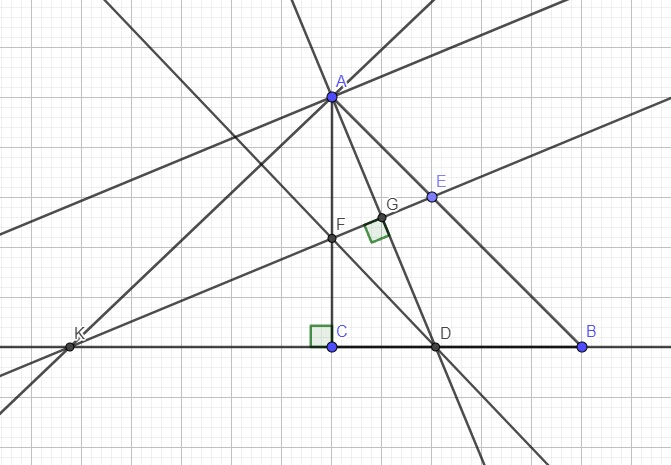
Dễ dàng nhận ra \(DF\perp AK\), từ đó biết vtpt của DF \(\Rightarrow\) phương trình DF
\(\Rightarrow\) Tọa độ F (là giao của DF và đường tròn tâm D bán kính DE do DE=DF)
Biết tọa độ F \(\Rightarrow\) viết được pt AD qua D vuông góc EF
\(\Rightarrow\) Tọa độ A từ là giao AK và AD
\(\Rightarrow\) Phương trình AB qua A và E, phương trình AC qua A và F, phương trình BC qua D và vuông góc AF
16 tháng 3 2020
a) +)Xét tg ABD có: CE //BD(gt)
Áp dụng đl Ta-let, ta có:
AB/AC=AD/AE
+) Xét tam giác ADC có: FE // CD(gt)
Áp dụng đl Ta-let,ta có:
AC/AF=AD/AE
b)Từ câu a), ta có:
AB/AC=AC/AF
->AC.AC=AB.AF
->AC^2=AB.AF