 làm hộ câu b,c,d thôi ạ
làm hộ câu b,c,d thôi ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 12:
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN


a. \(f\left(x\right)_{max}=f\left(-2\right)=111\) ; \(f\left(x\right)_{min}=f\left(1\right)=-6\)
b. \(f\left(x\right)_{max}=f\left(-3\right)=7\) ; \(f\left(x\right)_{min}=f\left(0\right)=1\)
c. \(f\left(x\right)_{max}=f\left(4\right)=\dfrac{2}{3}\) ; \(f\left(x\right)_{min}\) ko tồn tại
d.
Miền xác định: \(D=\left[-2\sqrt{2};2\sqrt{2}\right]\)
\(y'=\dfrac{2\left(4-x^2\right)}{\sqrt{8-x^2}}=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)
\(f\left(-2\sqrt{2}\right)=f\left(2\sqrt{2}\right)=0\)
\(f\left(-2\right)=-4\) ; \(f\left(2\right)=4\)
\(f\left(x\right)_{max}=f\left(2\right)=4\) ; \(f\left(x\right)_{min}=f\left(-2\right)=-4\)

10: Chọn B
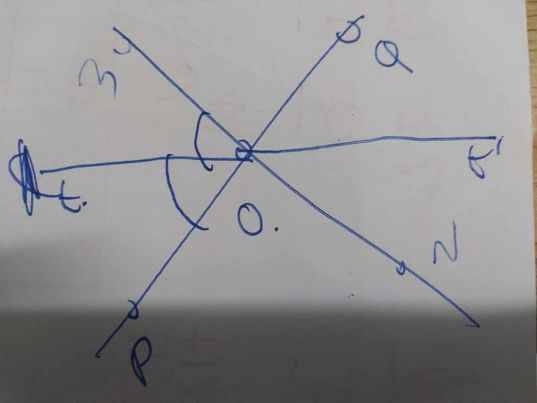
Ot là phân giác của \(\widehat{MOP}\)
=>\(\widehat{MOP}=2\cdot\widehat{tOP}\)
\(\widehat{MOP}=\widehat{NOQ}\)
=>\(\widehat{NOQ}=2\cdot\widehat{tOP}\)
mà \(\widehat{tOP}=\widehat{t'OQ}\)(hai góc đối đỉnh)
nên \(\widehat{NOQ}=2\cdot\widehat{t'OQ}\)
=>Ot' là phân giác của góc NOQ
11:
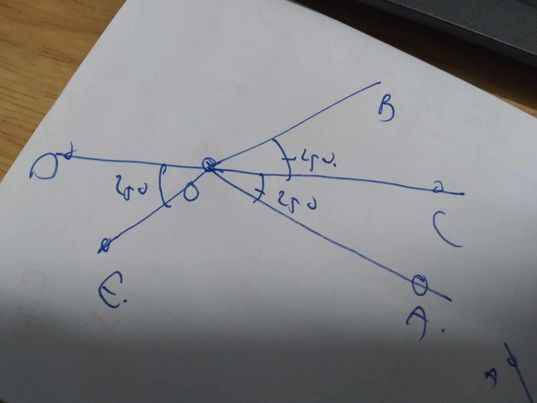
OC là phân giác của góc AOB
=>\(\widehat{AOC}=\widehat{BOC}=\dfrac{50^0}{2}=25^0\)
\(\widehat{DOE}=\widehat{BOC}\left(=25^0\right)\)
=>\(\widehat{DOE}+\widehat{DOB}=180^0\)
=>OB và OE là hai tia đối nhau
=>Hai góc đối đỉnh là \(\widehat{BOC};\widehat{DOE}\)
=>Chọn D
12:
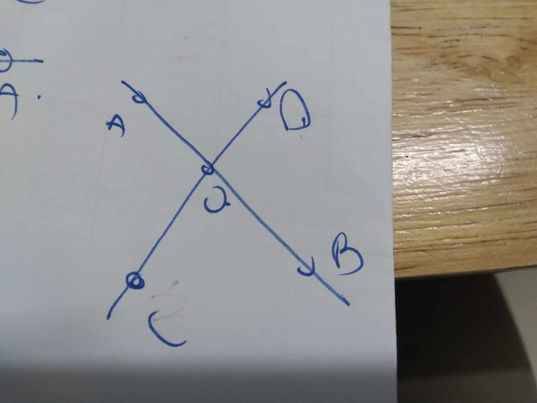
\(\widehat{AOC}+\widehat{AOD}=180^0\)
\(\widehat{AOC}-\widehat{AOD}=50^0\)
Do đó: \(\widehat{AOC}=\dfrac{180^0+50^0}{2}=115^0;\widehat{AOD}=115^0-50^0=65^0\)
=>\(\widehat{BOC}=\widehat{AOD}=65^0\)
=>Chọn B

(O) và (D) cắt nhau tại A và M \(\Rightarrow AM\perp OD\)
\(\Rightarrow\widehat{AOD}=\widehat{ABN}\) (cùng phụ \(\widehat{BAM}\))
\(\Rightarrow OD||BN\) (góc đồng vị bằng nhau)
\(\Rightarrow OBND\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow OB=DN\), mà \(\left\{{}\begin{matrix}AB=DC\\OB=\dfrac{1}{2}AB\end{matrix}\right.\) \(\Rightarrow OB=\dfrac{1}{2}CD\Rightarrow DN=\dfrac{1}{2}DC\Rightarrow N\) là trung điểm CD



a: góc OBA+góc OCA=90+90=180 độ
=>ABOC nội tiếp
b: góc OIE=góc OCE=90 độ
=>OICE là tứ giác nội tiếp
=>góc OEI=góc OCI
=>góc OEI=góc OCB
OBAC nội tiếp
=>góc OCB=góc OAB
=>góc OEI=góc OAB
=>góc OEI=góc OAI
=>OIAE nội tiếp



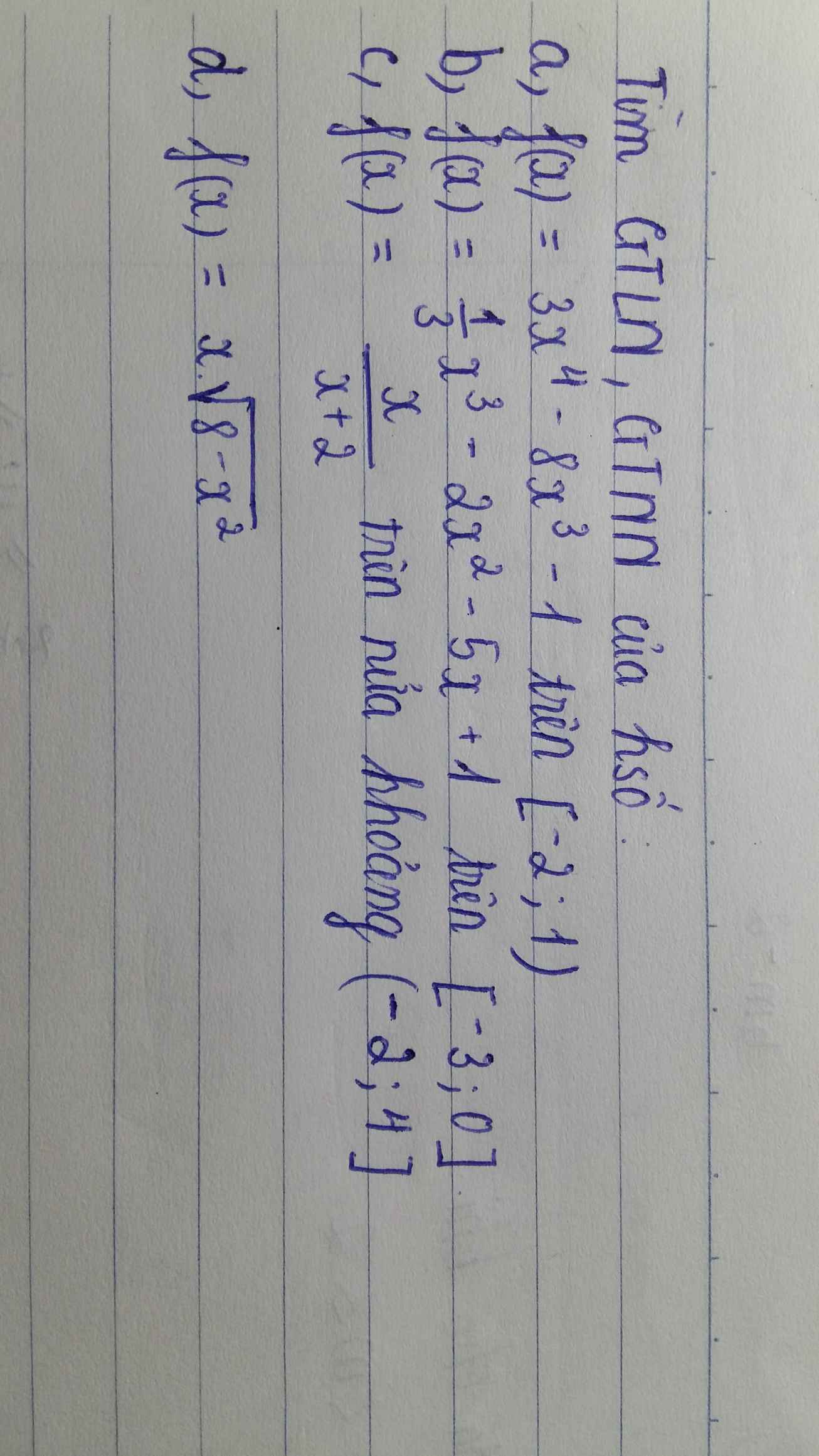
 làm câu 10,11,12 chỉ vẽ hình thôi nếu giải thì giải hộ ạ
làm câu 10,11,12 chỉ vẽ hình thôi nếu giải thì giải hộ ạ


 Like cho mình nhé !!
Like cho mình nhé !!


b: \(=\dfrac{x^2-x+1-3+1-x^2}{\left(x+1\right)\cdot\left(x^2-x+1\right)}=\dfrac{-x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{-1}{x^2-x+1}\)